😆
👉DISTRIBUCION UNIFORME: En las distribuciones continuas se suele comenzar con un modelo sencillo, pero de gran importancia en diferentes áreas de estudio en donde las variables aleatorias se distribuyen uniformemente en un intervalo finito (a,b) ó (a,b). Un modelo probabilístico continuo es de tipo uniforme, cuando la variable aleatoria continua que en él se define está distribuida en el intervalo (a,b) de tal forma que la probabilidad en un subintervalo cualesquiera, depende sólo de la longitud. Por consiguiente, su función de densidad dependerá de los valores de sus parámetros a y b. Formalizando el modelo tendremos lo siguiente.
V=(x)=\frac{(b-a^{2})}{12})
FUNCIÓN DE DISTRIBUCIÓN
F(x)=\begin{Bmatrix}&space;0&&space;x<&space;a&space;&&space;\\&space;\frac{x-a}{b-a}&&space;a\leq&space;x<&space;b&space;&&space;\\&space;1&&space;x\geq&space;b&space;&&space;\end{Bmatrix})
DEMOSTRACIÓN DE LAS FORMULAS DE LA DISTRIBUCIÓN UNIFORME
Empleando las formulas para el valor esperado, la variancia y la función de distribución acumulada de una variable aleatoria continua.
DEMOSTREMOS LA EXPRESIÓN PARA LA VARIANZA
EJERCICIOS RESUELTOS
👉 Problema 01: 😆
Sea la variable aleatoria continua la corriente medida, en miliamperes,en un alambre delgado de cobre. supongase que el rango de
la corriente medida, en miliamperes,en un alambre delgado de cobre. supongase que el rango de  es
es ![\bg_black \left [ 0,20 \right ]](https://latex.codecogs.com/gif.latex?\bg_black&space;\left&space;[&space;0,20&space;\right&space;]) mA y que la función de densidad de probabilidad de
mA y que la función de densidad de probabilidad de  es
es =0.05) ,
, 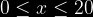 .
.
a)¿Cual es la probabilidad de que una medición de corriente este entre 5 y 10 miliamperes?
b) Obtenga la media y la varianza de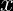
Solución Inciso a)
![\bg_black f(x)=\left\{\begin{matrix} \frac{1}{20-0} &x\epsilon \left [ 0,20 \right ]=\left\{\begin{matrix} \frac{1}{20}, & x\epsilon \left [ 0,20 \right ]\\ 0& \end{matrix}\right. \\ 0,& x\epsilon \left [ 0,20 \right ]x\epsilon \left [ 0,20 \right ] \end{matrix}\right.](https://latex.codecogs.com/gif.latex?\dpi{150}&space;\bg_black&space;f(x)=\left\{\begin{matrix}&space;\frac{1}{20-0}&space;&x\epsilon&space;\left&space;[&space;0,20&space;\right&space;]=\left\{\begin{matrix}&space;\frac{1}{20},&space;&&space;x\epsilon&space;\left&space;[&space;0,20&space;\right&space;]\\&space;0&&space;\end{matrix}\right.&space;\\&space;0,&&space;x\epsilon&space;\left&space;[&space;0,20&space;\right&space;]x\epsilon&space;\left&space;[&space;0,20&space;\right&space;]&space;\end{matrix}\right.)
La probabilidad se calcula por:
=\frac{1}{20}\int_{5}^{10}dx=\frac{10-5}{20}=\frac{5}{20}=0.25)
=\frac{a+b}{2}=\frac{0+20}{2}=\frac{20}{2}=10mA)
=\frac{(b-a^{2})}{12}=\frac{(20-0^{2})}{12}=\frac{20^{2}}{12}=33.33mA^{2})
👉 Problema 02: 😆
Suponga un experimento en el que de alguna manera se hace medición al azar y esta tiene una distribución uniforme en el intervalo![\left [ 0,3 \right ]](https://latex.codecogs.com/png.latex?\bg_black&space;\left&space;[&space;0,3&space;\right&space;]) . Calcule la probabilidad de que la medición
. Calcule la probabilidad de que la medición
este entre 1.5 y 2.
a) Por medio de su función de densidad.
b)Por medio de su función acumulada.
Solución Inciso a)
a) Sea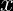 la variable aleatoria continua definida en el experimento, se ha mencionado en las condiciones del problema que
la variable aleatoria continua definida en el experimento, se ha mencionado en las condiciones del problema que 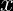 tiene una distribución en
tiene una distribución en ![\left [ 0,3 \right ]](https://latex.codecogs.com/png.latex?\bg_black&space;\left&space;[&space;0,3&space;\right&space;]) . Por lo tanto, su función de densidad estará dada por:
. Por lo tanto, su función de densidad estará dada por:
![\bg_black f(x)=\left\{\begin{matrix} \frac{1}{3-0} &x\epsilon \left [ 0,3 \right ]=\left\{\begin{matrix} \frac{1}{3}, & x\epsilon \left [ 0,3 \right ]\\ 0& \end{matrix}\right. \\ 0,& x\epsilon \left [ 0,3 \right ]x\epsilon \left [ 0,3 \right ] \end{matrix}\right.](https://latex.codecogs.com/gif.latex?\dpi{150}&space;\bg_black&space;f(x)=\left\{\begin{matrix}&space;\frac{1}{3-0}&space;&x\epsilon&space;\left&space;[&space;0,3&space;\right&space;]=\left\{\begin{matrix}&space;\frac{1}{3},&space;&&space;x\epsilon&space;\left&space;[&space;0,3&space;\right&space;]\\&space;0&&space;\end{matrix}\right.&space;\\&space;0,&&space;x\epsilon&space;\left&space;[&space;0,3&space;\right&space;]x\epsilon&space;\left&space;[&space;0,3&space;\right&space;]&space;\end{matrix}\right.)
La probabilidad se calcula por:
=\frac{1}{3}\int_{1.5}^{2}dx=\frac{2-1.5}{3}=\frac{1}{6})
👉 Problema 03: 😆
Suponga un experimento en el que de alguna manera se hace una medición al azar y esta puede estar distribuida uniformemente en el intervalo![\left [ 0,3 \right ]](https://latex.codecogs.com/png.latex?\bg_black&space;\left&space;[&space;0,3&space;\right&space;]) , Se realizan cinco mediciones independientes.
, Se realizan cinco mediciones independientes.
¿cuál es la probabilidad de que exactamente dos de ellas estén entre 1 y 2?
Solución Inciso a)
Primero definimos a la variable aleatoria continua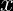 de forma similar que en el ejemplo anterior, para una sola medicion, en donde ella tiene una distribución uniforme en
de forma similar que en el ejemplo anterior, para una sola medicion, en donde ella tiene una distribución uniforme en ![\left [ 0,3 \right ]](https://latex.codecogs.com/png.latex?\bg_black&space;\left&space;[&space;0,3&space;\right&space;]) , y calculamos la probabilidad de que dicha medida se encuentre entre 1 y 2.
, y calculamos la probabilidad de que dicha medida se encuentre entre 1 y 2.
=\frac{2-1}{3-0}=\frac{1}{3})
Posteriormente definimos a la variable discreta, Y: " Cantidad de mediciones que resultan entre 1 y 2"
Ahora note que en este caso se tienen 5 ensayos independientes con probabilidad de éxito igual a:
=\frac{1}{3}\rightarrow&space;fracaso\rightarrow&space;\frac{2}{3})
Por lo tanto, se trata de un modelo binomial con parámetros:

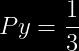
Así
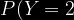=c_{2}^{5}\left&space;(&space;\frac{1}{3}&space;\right&space;)^{2}\left&space;(&space;\frac{2}{3}&space;\right&space;)^{3}=10\cdot&space;\frac{8}{243}=0.3292)
👉 Problema 04: 😆
👉 Problema 06: 😆
Un ingeniero estima inicialmente que el tiempo -en minutos- de maquinado de una pieza se modela con una distribución uniforme (10,20). Calcula la probabilidad de que:
a) Una pieza sea maquinada en menos de 14.5 minutos.
Solución Inciso a)
👉 Problema 07: 😆
Solución Inciso a)
Suponga que 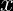 tiene una distribución uniforme continua en el intervalo
tiene una distribución uniforme continua en el intervalo ![\bg_black \left [ -1,1 \right ]](https://latex.codecogs.com/gif.latex?\bg_black&space;\left&space;[&space;-1,1&space;\right&space;]) .
.
a) Calcule la media y la varianza de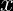 .
.
=\frac{a+b}{2}=\frac{-1+1}{2}=\frac{0}{2}=0)
=\frac{(b-a^{2})}{12}=\frac{(1-(-1)^{2})}{12}=\frac{2^{2}}{12}=0.3333)
👉 Problema 09: 😆
Considere una variable aleatoria cuya distribución es uniforme en el intervalo![\bg_black \left [ 0,1 \right ]](https://latex.codecogs.com/gif.latex?\bg_black&space;\left&space;[&space;0,1&space;\right&space;]) como se ha
como se ha
presentado es decir=b-a) siempre que
siempre que 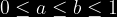 , con
, con
=P(x%3E&space;1)=0) se dice que la variable aleatoria
se dice que la variable aleatoria 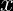 sigue una distribución uniforme
sigue una distribución uniforme
![\bg_black \left [ 0,1 \right ]](https://latex.codecogs.com/gif.latex?\bg_black&space;\left&space;[&space;0,1&space;\right&space;]) y se representa por
y se representa por 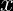 uniforme
uniforme ![\bg_black \left [ 0,1 \right ]](https://latex.codecogs.com/gif.latex?\bg_black&space;\left&space;[&space;0,1&space;\right&space;])
por ejemplo:
=\frac{3-1}{4-2}=\frac{1}{4})
👉 Problema 10: 😆
Supongamos que la variable aleatoria continua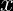 , tiene una distribución de tipo uniforme con su valor mas grande igual a 6 y valor esperado de 4.
, tiene una distribución de tipo uniforme con su valor mas grande igual a 6 y valor esperado de 4.
a) ¿Calcule el valor de a del valor esperado?
b) ¿Calcule la variancia de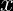 ?
?
Solución Inciso a)
Formula:
=\frac{a+b}{2})
Sustituyendo los valores de la formula:
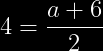
Despejando a:
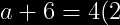)
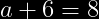
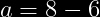

Solución Inciso b)
=\frac{(b-a^{2})}{12}=\frac{(6-2^{2})}{12}=\frac{4^{2}}{12}=1.3333)
Si x en una variable aleatoria continua del experimento realizado diremos que tiene una distribución uniforme con parámetros a y b , cuando su función de densidad de probabilidad esta distribuida en el intervalo (a,b)
FUNCIÓN DE DENSIDAD
Facilmente se comprueba que efectivamente la funcion anterior es una funcion de densidad de probabilidad puesto que no es negativa y la integral en todos los numeros reales vale uno.
El calculo de dicha integral se reduce al area del rectangulo con base igual a:
Si x es una variable aleatoria continua con distribucion uniforme en (a,b) y , f(x) es su funcion de densidad de probabilidad, entonces
ESPERANZA MATEMÁTICA LLAMADO TAMBIÉN VALOR ESPERADO
DESVIACIÓN ESTÁNDAR LLAMADO TAMBIÉN VARIANZA
FUNCIÓN DE DISTRIBUCIÓN
DEMOSTRACIÓN DE LAS FORMULAS DE LA DISTRIBUCIÓN UNIFORME
Empleando las formulas para el valor esperado, la variancia y la función de distribución acumulada de una variable aleatoria continua.
DEMOSTRACIÓN DE LA FORMULA DEL VALOR ESPERADO
DEMOSTREMOS LA EXPRESIÓN PARA LA VARIANZA
EJERCICIOS RESUELTOS
👉 Problema 01: 😆
Sea la variable aleatoria continua
a)¿Cual es la probabilidad de que una medición de corriente este entre 5 y 10 miliamperes?
b) Obtenga la media y la varianza de
Solución Inciso a)
La probabilidad se calcula por:
Solución Inciso b)
👉 Problema 02: 😆
Suponga un experimento en el que de alguna manera se hace medición al azar y esta tiene una distribución uniforme en el intervalo
este entre 1.5 y 2.
a) Por medio de su función de densidad.
b)Por medio de su función acumulada.
Solución Inciso a)
a) Sea
La probabilidad se calcula por:
Solución Inciso b)
👉 Problema 03: 😆
Suponga un experimento en el que de alguna manera se hace una medición al azar y esta puede estar distribuida uniformemente en el intervalo
¿cuál es la probabilidad de que exactamente dos de ellas estén entre 1 y 2?
Solución Inciso a)
Primero definimos a la variable aleatoria continua
Posteriormente definimos a la variable discreta, Y: " Cantidad de mediciones que resultan entre 1 y 2"
Ahora note que en este caso se tienen 5 ensayos independientes con probabilidad de éxito igual a:
Por lo tanto, se trata de un modelo binomial con parámetros:
Así
👉 Problema 04: 😆
La cantidad total de gasolina bombeada en un mes es una variable aleatoria X (expresada en diez miles de galones )con una función de densidad de probabilidad como se indica abajo.
b) determine la desviación estándar de los galones bombeados para un mes determinado.
Solución Inciso a)
Función de Densidad
Distribución Uniforme (0,3)
La integral Indefinida es :
y la probabilidad
Solución Inciso b)
Se calcula la desviación estándar de los galones bombeados para un mes determinado:
👉 Problema 05: 😆
Las ventas de combustibles en una gasolinera tienen una media de 40 000 litros por día y un mínimo de 30 000 litros por día. Supongamos que una distribución uniforme es apropiada.
a)Determine las ventas máximas diarias
b)¿Que porcentaje de días las ventas excederán de 34 000 litros?
Solución Inciso a)
Sustituyendo los valores de la formula:
Despejando b :
Solucion Inciso b)
👉 Problema 06: 😆
a) Una pieza sea maquinada en menos de 14.5 minutos.
Solución Inciso a)
La distribución uniforme tiene una función de probabilidad de:
La probabilidad Acumulada
Formula:
En este caso :
Sustituyendo los valores de la formula nos queda:
👉 Problema 07: 😆
Solución Inciso a)
👉 Problema 08: 😆
a) Calcule la media y la varianza de
Solución Inciso a)
👉 Problema 09: 😆
Considere una variable aleatoria cuya distribución es uniforme en el intervalo
presentado es decir
por ejemplo:
👉 Problema 10: 😆
Supongamos que la variable aleatoria continua
a) ¿Calcule el valor de a del valor esperado?
b) ¿Calcule la variancia de
Solución Inciso a)
Formula:
Sustituyendo los valores de la formula:
Despejando a:
Solución Inciso b)
👉 Problema 11: 😆
Un satélite que ha cumplido su ciclo en orbita alrededor de la tierra esta a punto de caer en ella, los especialistas calcularon su caída en algún lugar entre los puntos P y Q. Si su comportamiento es uniforme. Calcule la probabilidad de que la distancia con respecto a P sea mas de 4 veces la distancia con respecto a Q.
Solución Inciso a)
Por lo tanto, si calculamos la probabilidad requerida por una división entre segmentos tendremos: