👉DISTRIBUCION HIPERGEOMETRICA
Un experimento aleatorio se llama Hipergeométrico si cumple con las condiciones:
1- El experimento se realiza considerando un lote de tamaño N en el cual sus elementos están divididos en dos clases de tamaños m y N-m.
2- Se toma una muestra de tamaño n, sin remplazo, del lote.
3- Se calculan las probabilidades cuando k elementos de una de las clases estén en la muestra de tamaño n.
Si 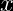 es una variable hipergeometrica con m éxitos en una población de tamaño N de la cual se elige una muestra sin reemplazo de tamaño n: entonces:
es una variable hipergeometrica con m éxitos en una población de tamaño N de la cual se elige una muestra sin reemplazo de tamaño n: entonces:
ESPERANZA MATEMÁTICA LLAMADO TAMBIÉN VALOR ESPERADO
DESVIACIÓN ESTÁNDAR LLAMADO TAMBIÉN VARIANZA
EJERCICIOS RESUELTOS
En un lote de 10 componentes electrónicos de TV en buen estado, se agregan 3 defectuosos, todos en apariencia y tamaños iguales.
Una persona compra 4 de tales componentes para reparar televisores.
a) Calcule la probabilidad de que la persona tenga que regresar a reclamar al vendedor, por haber obtenido componentes defectuosos.
Es un caso de distribución hipergeometrica:
Solución Inciso a)
La distribución hipergeometrica tiene por:
Formula:
Sustituyendo los valores de la formula:
👉 Problema 02: 😆
Un producto industrial particular se envía en lotes de 20. El análisis para determinar si un articulo tiene defecto es costoso, por tanto, el fabricante muestrea la producción en vez de usar un plan con el que tenga que inspeccionar el 100 %.
Un plan de muestreo construido para reducir el numero de artículos defectuosos enviados a los clientes requiere muestrear 5 artículos de cada lote y rechazarlo si se observa mas de 1 articulo defectuoso.(Si el lote se rechaza, entonces se prueba cada uno de los artículos.)Si en un lote hay 4 artículos defectuosos.¿cual es la probabilidad de que sea aceptado?
Es un caso de distribución hipergeometrica:
Solución Inciso a)
La distribución hipergeometrica tiene por:
Formula:
Sustituyendo los valores de la formula:
La probabilidad de aceptar el lote es;
La suma de esto nos da la probabilidad de:
La probabilidad del lote es del
👉 Problema 03: 😆
5 fabricantes producen en determinado dispositivo cuya calidad varia de un fabricante a otro. si usted elige 3 fabricantes al azar, hallar la probabilidad que la selección contenga 2 de las 3 mejores.
Es un caso de distribución hipergeométrica:
Solución Inciso a)
La distribución hipergeometrica tiene por:
Formula
Sustituyendo los valores de la Formula:
👉 Problema 04: 😆
En un lote de 10 proyectiles se disparan 4 al azar si el lote contiene 5 proyectiles que no disparan.
a)¿Cual es la probabilidad de que los 4 disparen?
b)¿Cuantos de los 4 se espera que disparen?
Solución Inciso a)
La distribución hipergeometrica tiene por
Formula
Sustituyendo los valores de la Formula:
Solución Inciso b)
Formula
Sustituyendo los valores de la Formula:
En Una oficina donde se ensamblan computadoras, en una mesa hay 20 chips de los cuales 6 están malogrados. Primero llega el Sr. Gates y recoge 8 chips y más tarde llega el Sr. Apple y se lleva los restantes. Halle la probabilidad que solamente uno de ellos se haya llevado todos los chips defectuosos.
Solución Inciso a)
La distribución hipergeometrica tiene por
Formula
Usamos una distribución hipergeometrica.
Sustituyendo los valores de la Formula:
Que solamente uno de ellos se lleve todos los chips es que:
La suma de esto nos da la probabilidad de 0.0245
👉 Problema 06: 😆
Una caja de vino tiene 12 botellas, tres de las cuales contienen vino descompuesto de la caja se elije al azar una muestra de 4 botellas.
a) Encuentre la distribución de probabilidad para 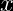 , el numero de botellas de vino echadas a perder en la muestra.
, el numero de botellas de vino echadas a perder en la muestra.
Solución Inciso a)
La distribución hipergeometrica tiene por
Formula:
Sustituyendo los valores de la Formula:
Solución Inciso b)
Formula
Sustituyendo los valores de la formula:
Formula para la varianza
Sustituyendo los valores de la formula:
👉 Problema 07: 😆
En una caja se tienen 20 discos duros para computadora colocados en forma vertical sin poner uno encima del otro.
Supóngase que entre los 20 existen 3 defectuosos,se seleccionan 4 de ellos aleatoriamente.
Solución Inciso a)
La distribución hipergeometrica tiene como
Formula:
Sustituyendo los valores de la formula:
👉 Problema 08: 😆
Una de las maquinas para elaborar tornillos milimétricos se descompuso y el fabricante se ha quedado con un gran numero de tornillos defectuosos.
Para tratar de evitar perdidas el proveedor de tornillos en cada caja de 30 tornillos coloca 5 defectuosos (25 buenos).
El vendedor de tornillos comienza a recibir reclamos por los defectuosos, y decide lo siguiente.
a) Cambiar de proveedor si al inspeccionar aleatoriamente 6 tornillos de la siguiente caja resultan dos o mas tornillos defectuosos en ella.
b) Cambiar de proveedor, si antes del cuarto de los siguientes envíos recibe una caja de tal forma que al inspeccionar aleatoriamente 6 tornillos resultan dos o mas tornillos defectuosos en ella.
En cada uno de los incisos anteriores, calcule la probabilidad de que el vendedor cambie de proveedor.
Considere que el proveedor no sabe nada de los planes del vendedor y sigue colocando 5 tornillos defectuosos por caja.
Solución Inciso a)
La distribución hipergeometrica tiene como
Formula: