😆
👉DISTRIBUCION DE POISSON: Este modelo estudia los experimentos cuyos resultados tienen lugar en intervalos continuos, de tiempo,áreas,volúmenes, etc.
Condiciones que debe cumplir un proceso de poisson
1- Los resultados de intervalos que no tienen puntos en común, son independientes.
Esto es, los resultados que ocurren en) son independientes de los que transcurren en el intervalo
son independientes de los que transcurren en el intervalo ) cuando los intervalos son disjuntos. Se dice que el experimento de poisson en su ejecución no tiene memoria.
cuando los intervalos son disjuntos. Se dice que el experimento de poisson en su ejecución no tiene memoria.
2- La probabilidad, de que en un resultado ocurra en un intervalo de tiempo mucho muy pequeño
) es una cantidad de orden
es una cantidad de orden 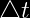 . Esto es, la probabilidad de obtener exactamente un resultado en un intervalo, suficientemente pequeño, es proporcional a la longitud del intervalo.
. Esto es, la probabilidad de obtener exactamente un resultado en un intervalo, suficientemente pequeño, es proporcional a la longitud del intervalo.
3- La probabilidad de que ocurra mas de un resultado en el transcurso del intervalo)
es una cantidad mucho mas pequeña en comparación con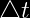 .
.
Esto significa que la probabilidad de obtener 2 ó mas resultados en un intervalo sumamente pequeño es despreciable.
👉 Problema 01: 😆
En una clínica el promedio de atención es 16 pacientes por 4 horas, encuentre la probabilidad que en 30 minutos se atiendan menos de 3 personas y que en 180 minutos se atiendan 12 pacientes.
Usamos la distribución de Poisson
👉 Problema 04: 😆
Los reportes de crímenes recientes indican que 3.2 de los robos de vehículos motorizados ocurren cada minuto en estados unidos. Suponga que la distribución de los robos por minuto puede calcularse con la distribución de probabilidad de poisson.
Este modelo tiene muchas aplicaciones. Se emplea generalmente en donde, se desea optimizar los tiempos, tanto de espera como de servicio, a este tipo de problemas se les estudia en el área de investigación de operaciones en Lineas de Espera o Teorías de Colas.
Condiciones que debe cumplir un proceso de poisson
1- Los resultados de intervalos que no tienen puntos en común, son independientes.
Esto es, los resultados que ocurren en
2- La probabilidad, de que en un resultado ocurra en un intervalo de tiempo mucho muy pequeño
3- La probabilidad de que ocurra mas de un resultado en el transcurso del intervalo
es una cantidad mucho mas pequeña en comparación con
Esto significa que la probabilidad de obtener 2 ó mas resultados en un intervalo sumamente pequeño es despreciable.
EJERCICIOS RESUELTOS
👉 Problema 01: 😆
En una clínica el promedio de atención es 16 pacientes por 4 horas, encuentre la probabilidad que en 30 minutos se atiendan menos de 3 personas y que en 180 minutos se atiendan 12 pacientes.
Usamos la distribución de Poisson
👉 Problema 02: 😆
👉 Problema 03: 😆
👉 Problema 04: 😆
Los reportes de crímenes recientes indican que 3.2 de los robos de vehículos motorizados ocurren cada minuto en estados unidos. Suponga que la distribución de los robos por minuto puede calcularse con la distribución de probabilidad de poisson.
a)¿calcule la probabilidad de que ocurran cuatro robos exactamente en un minuto.
b)¿cuál es la probabilidad de que en un cuarto de hora cualquiera ocurran exactamente 45 robos?
👉 Problema 05: 😆
Suponga que la agencia de protección ambiental (APA) es quien establece los estándares para Garantizar la calidad de las emisiones de aire por parte de las empresas. El límite máximo Permitido de cobre en las emisiones es de 10 partículas por millón y usted trabaja en una empresa Donde el valor medio en sus emisiones es de cuatro partículas por millón.
Suponga que la agencia de protección ambiental (APA) es quien establece los estándares para Garantizar la calidad de las emisiones de aire por parte de las empresas. El límite máximo Permitido de cobre en las emisiones es de 10 partículas por millón y usted trabaja en una empresa Donde el valor medio en sus emisiones es de cuatro partículas por millón.
a) Si se define X como el número de partículas por millón en una muestra ¿Cuál es la desviación estándar de X en su empresa?
b) Si el número medio de partículas por millón en su empresa es efectivamente de cuatro por millón ¿Tendría usted temor de que la agencia lo multe por contaminar el aire?














