"De acuerdo con National Geographic el 32% de los australianos que viven en el interior beben "tinnies" una cerveza local. De los 500 australianos seleccionados aleatoriamente, ¿Cuál es la probabilidad de que por lo menos 150 hayan bebido una tinnie?
Aplicas la distribución binomial por la normal.
Formula: z=(x-μ)/σ
p=0.32 Binomial por normal
q=0.68 a)p(x≤150) p(x≤150.5) ←corrección de continuidad.
n=500
E(x)=n.p=500(0.32)=160 v(x)=n.p.q=500(0.32)(0.68)=√108.8
σ=10.43
Aplicando la formula: z=(150.5-160)/10.43=-0.9108 buscando en las tablas.
Redondeando: -0.91 =0.1814←valor de las tablas.
a)p(x≤150)= 0.1814 esta es la probabilidad de que por lo menos 150 hayan bebido una tinnie.
--------------------------------------------------------------------------------------------------------------------------------------------------------------------
martes, 6 de octubre de 2009
lunes, 5 de octubre de 2009
DISTRIBUCIÓN NORMAL (2022) Ejemplos
EJERCICIOS RESUELTOS
👉 Problema 06: 😆
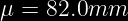
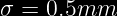
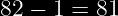
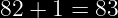
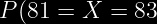)
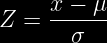
=0.9544)
Se sabe que la dimensión de una pieza se distribuye normal con media µ = 82.0 mm y σ=0.5mm
se desea calcular el porcentaje de piezas que cumplen con especificaciones 82 ± 1. μ = 82.0 ± 1.
Solución Inciso a)
En esta parte sumas y restas 1, por que las especificaciones nos marcan: 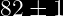
Por lo tanto:
Formula:
Ahora buscamos el valor en las tablas. Aplicando la formula:
❶ 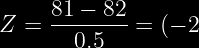=0.0228) Valor de tablas
Valor de tablas
❷ 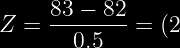=0.9772) Valor de tablas
Valor de tablas
Para sacar el porcentaje multiplicas por 100 = 0.9544 x100= 95.44 % piezas que cumplen con las especificaciones.
sábado, 3 de octubre de 2009
DISTRIBUCIÓN BINOMIAL (2022) Ejemplos
Suponga que para un embarque muy grande chips de circuitos integrados, la probabilidad de falla para cualquier chip es de 0,10. Suponga que se cumplen las suposiciones en que se basan las distribuciones binomiales ¿encuentre la probabilidad de que a lo más 3 chips fallen en una muestra aleatoria de 20?
la probabilidad de que a lo más 3 chips fallen es: 0.8668
--------------------------------------------------------------------------------------------------------------------------------------------------------------------
la probabilidad de que a lo más 3 chips fallen es: 0.8668
--------------------------------------------------------------------------------------------------------------------------------------------------------------------
Derivada de X COS X
Solución Inciso a)
Derivada
))
=v\frac{du}{dx}+u\frac{dv}{dx})
![https://latex.codecogs.com/png.image?\large \dpi{120}\bg{black}\frac{\mathrm{d} }{\mathrm{d} x}(x.cos(x))=cos(x)\left [ \frac{d(x)}{dx} \right ]+x\left [ \frac{d(cos(x))}{dx} \right ]](https://latex.codecogs.com/png.image?\large&space;\dpi{120}\bg{black}\frac{\mathrm{d}&space;}{\mathrm{d}&space;x}(x.cos(x))=cos(x)\left&space;[&space;\frac{d(x)}{dx}&space;\right&space;]+x\left&space;[&space;\frac{d(cos(x))}{dx}&space;\right&space;])
=1)
)=-sen(x))
![https://latex.codecogs.com/png.image?\large \dpi{120}\bg{black}\frac{\mathrm{d} }{\mathrm{d} x}(x.cos(x))=cos(x)\left [ 1 \right ]+x\left [ -sen(x) \right ]](https://latex.codecogs.com/png.image?\large&space;\dpi{120}\bg{black}\frac{\mathrm{d}&space;}{\mathrm{d}&space;x}(x.cos(x))=cos(x)\left&space;[&space;1&space;\right&space;]+x\left&space;[&space;-sen(x)&space;\right&space;])
)=1\bullet&space;cos(x)+(-sen(x))x)
)=cos(x)-xsen(x))
Aplicar la regla del producto:
Donde  and
and 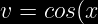)
Sustituyendo los valores en la regla del producto obtenemos:
Derivando los valores dentro de los corchetes obtendremos:
Quitando los corchetes nos queda:
Realizando las operaciones quitando paréntesis nos queda como resultado:
Suscribirse a:
Entradas (Atom)
