martes, 27 de diciembre de 2011
lunes, 26 de diciembre de 2011
sábado, 12 de marzo de 2011
DISTRIBUCION NORMAL (2022) Ejemplos
DISTRIBUCION NORMAL:
La Distribución Normal es una distribución de variables aleatorias continuas, que se utiliza mucho en aplicaciones de cálculo de probabilidades.
Es un modelo continuo con mayor aplicación en la probabilidad y la estadística; el modelo normal o distribución normal fue encontrada por Carl Friedrich Gauss por lo que se le conoce como: " Ley de Probabilidad de Gauss".
Definición: Sea X una variable aleatoria continua. Se dice que X tiene una distribución normal o de Gauss, con parámetros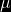 
y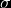 
(positivo) en todos los reales cuando su función de densidad de probabilidad es:
Los modelos de distribución normal se caracterizan por la forma de la grafica de su función de densidad, la grafica de la distribución normal tiene forma de campana como en la grafica siguiente:
Grafica Distribución Normal
El modelo de distribución normal tiene una gran aplicación en diferentes áreas y es una de las distribuciones con auge en las probabilidades y estadísticas, la dimensión de importancia radica en el "teorema de limite central "
TEOREMA:
Si X es una variable aleatoria continua distribuida normalmente en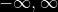 
y f(x) su función de densidad de probabilidad, entonces:
a) =\mu&space; "https://latex.codecogs.com/png.image?\dpi{110}\bg{black}E(X)=\mu")
b) =\sigma&space;^{2} "https://latex.codecogs.com/png.image?\dpi{110}\bg{black}V(X)=\sigma ^{2}")
PROPIEDADES DE LA DISTRIBUCION NORMAL ESTANDAR
a) Propiedad de Simetría: La función f(z) es simétrica con respecto al eje de las ordenadas. Es decir,
b) Propiedad del Complemento: En los casos de
c) =0.6827 "https://latex.codecogs.com/png.image?\dpi{110}\bg{black}P(-1< Z< 1)=0.6827")
d) =0.9545 "https://latex.codecogs.com/png.image?\dpi{110}\bg{black}P(-2< Z< 2)=0.9545")
e) La Suma de probabilidades fuera del intervalo  "https://latex.codecogs.com/png.image?\dpi{110}\bg{black}(-4,4)")
, no puede ser mayor a 0.0001,es decir, casi vale Cero.
EJERCICIOS RESUELTOS
👉 Problema 01:😆
👉 Problema 01:😆
Dada una variable aleatoria continua X, cuya distribución de probabilidad es  "https://latex.codecogs.com/png.image?\dpi{110}\bg{black}N(\mu ,\sigma )")
, en la que el 10.03 % del área bajo la curva está a la izquierda de x=60, y 5.05 % del área está a la derecha de x=90, determine los valores de la media y desviación estándar?
Solución Inciso a)
Para la solución de este ejercicio se Utiliza el Sistema de Ecuación de 2 incógnitas.
Estandarizamos mediante:
Despejamos:
Sustituimos los valores de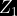 
y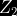 
en el despeje de la ecuación:
Haciendo las operaciones de la Ley de Signos, La primera Ecuación nos queda:
Sumando los valores de 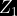y 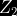de la Ecuación 1 y 2 nos queda:
Sustituyendo el valor de la desviación estándar en la segunda ecuación nos queda:
👉 Problema 1.1:😆
=0.11 "P(x\geq 5)")
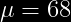
=1-0.11 "https://latex.codecogs.com/png.image?\large \dpi{110}\bg{black}1-P(Z> z)=1-0.11")
=0.89 "https://latex.codecogs.com/png.image?\large \dpi{110}\bg{black}P(Z> z)=0.89")
 "https://latex.codecogs.com/png.image?\large \dpi{120}\bg{black}P(70< X <75 )")
= "https://latex.codecogs.com/png.image?\large \dpi{120}\bg{black}P(0.4< Z< 1.4)=")
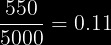
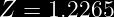
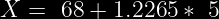
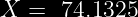
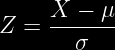
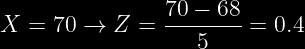
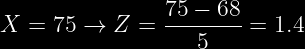
-P(Z%3C&space;0.4)&space;= "https://latex.codecogs.com/png.image?\large \dpi{120}\bg{black} P(Z< 1.4)-P(Z< 0.4) =")
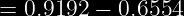
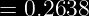
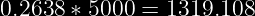
El peso de los estudiantes de una universidad se distribuye normalmente con un valor promedio de 68 kg y desviación estándar 5 kg.
Si se tienen 5000 estudiantes y los 550 estudiantes mas pesados serán sujetos a un examen medico.
a) ¿Cuál es el peso mínimo para someter un estudiante al examen?
b) Cuantos estudiantes de los 5000 se espera que pesen entre 70 y 75 kg.
Paso Número 1. debemos calcular el valor de Z tal que:
o lo que es lo mismo:
Solución Inciso a)
Buscando en el interior de la tabla de la distribución normal estandarizada  "https://latex.codecogs.com/png.image?\large \dpi{120}\bg{black}N\left ( 0, 1\right )")
el valor de Z es:
El valor de X es:
Es decir que el peso mínimo de los 550 estudiantes mas pesados es de 74.1325 Kg.
Solución Inciso b)
Estandarizamos mediante:
Por lo tanto:
Multiplicamos por los 5000 estudiantes
Se espera que unos 1319.108 estudiantes pesen entre 70 y 75 Kg.
Grafica
👉 Problema 1.2: 😆
Si =4&space; "https://latex.codecogs.com/png.image?\dpi{110}\bg{black}E(X)=4")
Y =9 "https://latex.codecogs.com/png.image?\dpi{110}\bg{black}V(X)=9")
; Calcule la probabilidad  "https://latex.codecogs.com/png.image?\dpi{110}\bg{black}P(X\geq 7)")
Para la solución de este problema de distribución normal aplicamos el teorema y nos dará el valor promedio de este ejercicio:
Teorema Aplicado =\mu&space; "https://latex.codecogs.com/png.image?\large \dpi{120}\bg{black}E(X)=\mu")
Datos del problema &space;=4 "https://latex.codecogs.com/png.image?\large \dpi{120}\bg{black}E(X) =4")
Valor promedio :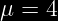 
Solución de la varianza aplicando nuevamente el teorema para que nos de la desviación estándar:
Teorema Aplicado &space;=\sigma&space;^{2} "https://latex.codecogs.com/png.image?\large \dpi{120}\bg{black}V(X) =\sigma ^{2}")
Datos del problema &space;=9 "https://latex.codecogs.com/png.image?\large \dpi{120}\bg{black}V(X) =9")
Desviación estándar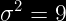 
Para esto, primero realizamos la estandarización de la variable X y después empleamos las tablas de la distribución normal estándar.
Solución Inciso a)
Estandarizamos mediante la Formula:
Grafica
👉 Problema 1.3: 😆
El peso de los estudiantes hombres de la UPIICSA se distribuye normalmente con un valor promedio de 70.5 kg y una desviación estándar de 5.3. Si los estudiantes que pesen mas de 85 kg. serán convocados para formar parte del equipo de Futbol Americano que representara a la escuela.
Determine el porcentaje de alumnos que podrán ser convocados.
Solución Inciso a)
Estandarizamos con:
Para sacar el porcentaje multiplicas por 100 = 0.0031 x 100= 0.31 % de alumnos que podrán ser convocados.
Grafica
👉 Problema 1.4: 😆
Si =3 "https://latex.codecogs.com/png.image?\dpi{100}\bg{black}E(X)=3")
Y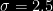 
; Calcule  "https://latex.codecogs.com/png.image?\dpi{110}\bg{black}P(-1< X< 5)")
Para la solución de este problema de distribución normal aplicamos el teorema y nos dará el valor promedio de este ejercicio:
Teorema Aplicado
Datos del problema =3 "https://latex.codecogs.com/png.image?\large \dpi{120}\bg{black}E(X)=3")
Valor promedio :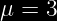 
Desviación estándar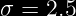 
Para esto, primero realizamos la estandarización de la variable X y después empleamos las tablas de la distribución normal estándar.
Solución Inciso a)
Estandarizamos mediante la Formula:
Grafica
👉 Problema 1.5: 😆
La Calificación de Matemáticas en una sección sigue una distribución normal con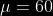 
y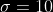 
Entre que valores estarán situadas el 95% central de las calificaciones?
Solución Inciso a)
El valor asociado a la tabla de probabilidad de 0.975 es
Estandarizamos con:
despejando
El valor asociado a la tabla de probabilidad de 0.025 es
Estandarizamos con:
despejando
Es decir que los valores centrales de las calificaciones son: 79.6 y 40.4
👉 Problema 1.6: 😆
Las calificaciones en un curso de estadística tienen una distribución normal con una media de 60 y una desviación estándar de 10. La probabilidad de que una persona elegida al azar tenga una calificación superior a 70 es?
Solución Inciso a)
Estandarizamos mediante:
Grafica
👉 Problema 1.7: 😆
El promedio del costo de una laptop es de $22000 con una desviación estándar de $7000. Si se considera que la distribución normal, encuentra la probabilidad de que una laptop cueste menos de $28000.
Solución Inciso a)
Estandarizamos mediante:
Grafica
👉 Problema 1.8: 😆
Las calificaciones en un curso de estadística tienen una distribución normal con una media de 60 y una desviación estándar de 10, el profesor decide que el 10% de los mejores estudiantes no presentan el parcial final. La calificación mínima que debe tener un estudiante para ser eximido del parcial es?
Solución Inciso a)
El valor asociado a la tabla de probabilidad de 0.95 es
Estandarizamos con:
despejando
Sustituyendo los valores de la formula nos queda:
👉 Problema 1.9: 😆
En un examen de estadística la media fue de 72 y la desviación estándar fue de 15 ¿Cuál fue la puntuación obtenida por un estudiante si su valor correspondió a Z=1,60?
Solución Inciso a)
Buscando en el interior de la tabla de distribución normal estandarizada el valor de Z es:
Estandarizamos con:
despejando el valor de X es:
Sustituyendo los valores en el despeje nos queda:
Por lo tanto la puntuación obtenida fue de 96
👉 Problema 1.10: 😆
Si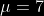 
Y 
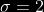Calcule; la probabilidad  "https://latex.codecogs.com/png.image?\dpi{110}\bg{black}P(X> 9)")
Solución Inciso a)
Estandarizamos con:
Grafica
👉 Problema 1.11: 😆
Los resultados de un examen siguen una distribución normal con media 7 y desviación típica 2. Se pide a)¿Cuál es la probabilidad de que un estudiante que se presenta al examen obtenga una calificación superior a 7?
Solución Inciso a)
Estandarizamos con:
Grafica
👉 Problema 1.12: 😆
El peso promedio de alguna población es de 74 kg y la desviación estándar es de 6 kg. Calcula el porcentaje de personas que pesan mas de 80 kg.
Solución Inciso a)
Estandarizamos con:
Para sacar el porcentaje multiplicas por 100 = 0.1587 x 100= 15.87 % es el porcentaje de personas que pesan mas de 80 kg.
Grafica
👉 Problema 1.13: 😆
Sea X una variable aleatoria normalmente distribuida, con media 1 y varianza 4. Calcular :
a)  "https://latex.codecogs.com/png.image?\dpi{110}\bg{black}P(X\geq 1)")
b)  "https://latex.codecogs.com/png.image?\dpi{110}\bg{black}P(X< 2)")
c)  "https://latex.codecogs.com/png.image?\dpi{110}\bg{black}P(0\leq X\leq 2)")
Solución Inciso a)
Solución de la varianza aplicamos el teorema para que nos de la desviación estándar:
Teorema Aplicado
Datos del problema =4 "https://latex.codecogs.com/png.image?\large \dpi{120}\bg{black}V(X)=4")
Desviación estándar 
Estandarizamos con:
Grafica
Solución Inciso b)
Estandarizamos con:
Grafica
Solución Inciso c)
Estandarizamos con:
Por lo tanto:
Grafica
👉 Problema 1.14: 😆
La media de los pesos de 700 estudiantes de una universidad es de 70 kg y la desviación típica 7 kg. Suponiendo que los pesos se distribuyen normalmente, Hallar cuantos estudiantes pesan:
a) Entre 55 kg y 65 kg b) Más de 80 kg c) Menos de 64 kg
d) 60 kg ó Menos
Solución Inciso a)
Estandarizamos con:
Por lo tanto:
Grafica
Para hallar cuantos estudiantes pesan Entre 55 kg y 65 kg Multiplicamos la probabilidad obtenida por los 700 estudiantes.
Por lo tanto 155.89 estudiantes pesan entre 55 kg y 65 kg.
Solución Inciso b)
Estandarizamos con:
Grafica
Para hallar cuantos estudiantes pesan Más de 80 kg Multiplicamos la probabilidad obtenida por los 700 estudiantes.
Por lo tanto 53.48 estudiantes pesan Más de 80 kg.
Suscribirse a:
Entradas (Atom)