El tiempo Y que tarda en realizarse cierta tarea clave en la construccion de una casa es una variable aleatoria que tiene una distribucion exponencial con una media de 10 horas.
El costo C para completar esta tarea esta relacionado con Y mediante
C = 100 + 40Y + 3Y2
Encontrar el valor esperado y la varianza de C.
f(y) = k e^(- k y) para y > 0
μ = ∫ k y e^(- k y) = 1/ k de 0 a infinito
μ = 10 ---> k = 0.1 ..........var(y) = 1/ k^2 = 1/ .01 = 100
El valor esperado de y^2
∫ .1y^2 e^( - .1y) = 200 de o a infinito
E(C) = 100+40 E(y) + 3 E(y^2)
E(C) = 100 + 40 (10) + 3 (200)
E(C) = 100 + 400 + 600 = 1100
Para la varianza me falta tiempo.
Var(C) = E ( C - E(C))^2
C - E(C) = 100 + 40 y + 3 y^2 - (100 + 40 E(y) + 3 E(y^2))
E(C - E(C))^2 =( 40 y + 3 y^2 - 40(10) + 3 (200) )^2
Var(C) = E(1000000 - 80000 y - 4400 y^2 + 240 y^3 + 9 y^4)
Var(C) = 1000000 -80000E(y) -4400E(y^2) + 240E(y^3) + 9E(y^4)
E(y^3)= ∫ .1y^3 e^( - .1y) = 6000 de o a infinito
E(y^4) = ∫ .1y^4 e^( - .1y) = 240000 de o a infinito
= 1000000 - 80000(10) - 4400(200) + 240(6000) + 9(240000)
Var(C) = 2 920 000
lunes, 2 de marzo de 2015
FRACCIONES
FRACCIÓN COMÚN: Es una expresión que representa una o varias partes de la unidad; también se le denomina "QUEBRADO".
Una fracción esta compuesta de dos números llamados términos de la fracción y separados entre si por medio de una lineal horizontal o diagonal.
Una fracción esta compuesta de dos números llamados términos de la fracción y separados entre si por medio de una lineal horizontal o diagonal.
El numero que va sobre la linea, se llama NUMERADOR
El que va por debajo de la linea, se llama DENOMINADOR
Ejemplo:
FRACCIÓN PROPIA: Su valor es menor a la unidad.
Ejemplo:
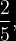
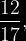
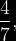

FRACCIÓN IMPROPIA: Su valor es mayor o igual que la unidad.
Ejemplo:
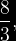
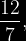
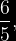

NUMERO MIXTO: Se llama numero mixto al que esta formado por una parte entera y una fraccionaria. Para transformar fracciones impropias en números mixtos, solo es necesario realizar la división.
DEFINICION DE NUMERADOR: Es el numero que indica cuantas unidades fraccionarias contiene la fracción.
DEFINICION DE DENOMINADOR: Es el numero que indica las partes iguales en que se ha dividido la unidad.
Las fracciones comunes se clasifican en fracción propia y fracción impropia.
FRACCIÓN PROPIA: Su valor es menor a la unidad.
Ejemplo:
FRACCIÓN IMPROPIA: Su valor es mayor o igual que la unidad.
Ejemplo:
EJERCICIOS RESUELTOS
👉 Problema 01: 😆
Transformar una fracción impropia a una mixta
👉 Problema 02: 😆
Transformar un numero mixto a una fracción impropia
Para la solución de este problema hacemos la multiplicación del denominador del numero mixto que es 7 por el numero entero que es 3 mas la suma del numerador que es 5 todo esto entre 7 la cual nos da como resultado en la imagen siguiente:
DISTRIBUCION EXPONENCIAL
El tiempo de recurrencia para el tratamiento de cierto tipo de cáncer es una variable aleatoria con una distribución exponencial con media λ. 50% de los pacientes tienen una recurrencia dentro de 693 días.
a)Encuentre λ
b)Encuentre la probabilidad de que un paciente que no ha tenido la recurrencia en el primer año después del tratamiento, tendrá la recurrencia durante el segundo año.
la distribución exponencial tiene por función de densidad:
f(x) = 1/λ * exp(-1/λ*x)
La función de distribución (probabilidad acumulada) es
P(X<=x) = F(X) = 1 - exp(-1/λ*x)
Nos dicen que
F(693) = 0.50
1 - exp(-1/λ*693) = 0.50
exp(-1/λ*693) = 1-0.50
exp(-1/λ*693) = 0.50
tomando logaritmos
ln { exp(-1/λ*693) } = ln 0.50
-1/λ*693 = ln 0.50
-693/λ = ln 0.50
λ = -693 / ln 0.50
λ = 999.77
b)
Es una probabilidad condicionada
P(365365) = P(365365)
365
por tanto la probabildad es
P(365X<730>365) =
donde
P(365X<730 -="" f="" p="">
P(X>365) = 1-F(365)
tenemos que
F(730) = 1-exp(-1/999.78*730) = 0.5182
F(365) = 1-exp(-1/999.78*365) = 0.3059
Por tanto
P(365X<730 -="" 0.3059="0.2123</p" 0.5182="" f="">
P(X>365) = 1-F(365) = 1-0.3059 = 0.6941
La probabilidad es 0.2123/0.6941 = 0.3058
a)Encuentre λ
b)Encuentre la probabilidad de que un paciente que no ha tenido la recurrencia en el primer año después del tratamiento, tendrá la recurrencia durante el segundo año.
la distribución exponencial tiene por función de densidad:
f(x) = 1/λ * exp(-1/λ*x)
La función de distribución (probabilidad acumulada) es
P(X<=x) = F(X) = 1 - exp(-1/λ*x)
Nos dicen que
F(693) = 0.50
1 - exp(-1/λ*693) = 0.50
exp(-1/λ*693) = 1-0.50
exp(-1/λ*693) = 0.50
tomando logaritmos
ln { exp(-1/λ*693) } = ln 0.50
-1/λ*693 = ln 0.50
-693/λ = ln 0.50
λ = -693 / ln 0.50
λ = 999.77
b)
Es una probabilidad condicionada
P(365
365
por tanto la probabildad es
P(365X<730>365) =
donde
P(365X<730 -="" f="" p="">
P(X>365) = 1-F(365)
tenemos que
F(730) = 1-exp(-1/999.78*730) = 0.5182
F(365) = 1-exp(-1/999.78*365) = 0.3059
Por tanto
P(365X<730 -="" 0.3059="0.2123</p" 0.5182="" f="">
P(X>365) = 1-F(365) = 1-0.3059 = 0.6941
La probabilidad es 0.2123/0.6941 = 0.3058
DISTRIBUCION EXPONENCIAL
La vida promedio de un televisor es de 12 años. La vida de los productos sigue con frecuencia, una distribucion exponencial de probabilidad suponga que es el caso del televisor.
Cual es la probabilidad de que la vida sea de 15 años o mas.
E(X)=1/λ
12=1/λ
λ=1/12
La formula de la distribución exponencial es
f(x)=λ*exp(-λx)
y la de probabilidad acumulada e
F(x)=1-exp(-λx) que representa a P(X≤x)
a)
Debemos calcular
P(X>15) = 1 - P(X≤15) = 1-F(15)
F(15)= 1-exp(-1/12*15) = 0.7135
por lo que
P(X>15) = 1-F(15) = 1-0.7135
P(X>15) = 0.2865
Cual es la probabilidad de que la vida sea de 15 años o mas.
E(X)=1/λ
12=1/λ
λ=1/12
La formula de la distribución exponencial es
f(x)=λ*exp(-λx)
y la de probabilidad acumulada e
F(x)=1-exp(-λx) que representa a P(X≤x)
a)
Debemos calcular
P(X>15) = 1 - P(X≤15) = 1-F(15)
F(15)= 1-exp(-1/12*15) = 0.7135
por lo que
P(X>15) = 1-F(15) = 1-0.7135
P(X>15) = 0.2865
FUNCIONES Y LIMITES
FUNCIÓN: Es el conjunto de pares ordenados de números reales (x,y) en los que el primer elemento es diferente en todos y cada uno de los pares ordenados.
Ejemplo:
1-A =(2,5)(3,6)(4,7)(5,8) Representa una función ya que el primer elemento de cada par ordenado es diferente de los otros.
2-B=(1,1)(1,-1)(4,2)(4,-2) No representa una función ya que se repite el primer elemento en ciertos pares ordenados.
REGLA DE CORRESPONDENCIA
Es la expresión que relaciona la variable dependiente con la variable independiente y se denota por:
y= F(x),se lee (y es igual a f de x )
Donde:
x: variable independiente
y:variable dependiente
F(x):regla de correspondencia
Ejemplo:
1-A =(2,5)(3,6)(4,7)(5,8) Representa una función ya que el primer elemento de cada par ordenado es diferente de los otros.
2-B=(1,1)(1,-1)(4,2)(4,-2) No representa una función ya que se repite el primer elemento en ciertos pares ordenados.
REGLA DE CORRESPONDENCIA
Es la expresión que relaciona la variable dependiente con la variable independiente y se denota por:
y= F(x),se lee (y es igual a f de x )
Donde:
x: variable independiente
y:variable dependiente
F(x):regla de correspondencia
DIVISIBILIDAD Y CALCULO DEL MAXIMO COMUN DIVISOR
DIVISIBILIDAD: Un numero es divisible entre otro cuando al dividir el primero entre el segundo, el cociente es exacto.
EJEMPLOS: La divisibilidad es la propiedad que tiene un numero para ser dividido entre otro exactamente.
CRITERIOS DE DIVISIBILIDAD: En ciertos casos no es necesario efectuar la división, basta seguir los criterios de divisibilidad que a continuación se señalan.
NUMERO PAR: Es todo numero que es múltiplo de 2
EJEMPLO: Son números pares: 2,4,6,8,10,12,14....etc
NUMERO IMPAR: Es todo numero que no es múltiplo de 2
EJEMPLO: Son números impares: 1,3,5,7,9,11,13,15.....etc
EJEMPLOS: La divisibilidad es la propiedad que tiene un numero para ser dividido entre otro exactamente.
CRITERIOS DE DIVISIBILIDAD: En ciertos casos no es necesario efectuar la división, basta seguir los criterios de divisibilidad que a continuación se señalan.
NUMERO PAR: Es todo numero que es múltiplo de 2
EJEMPLO: Son números pares: 2,4,6,8,10,12,14....etc
NUMERO IMPAR: Es todo numero que no es múltiplo de 2
EJEMPLO: Son números impares: 1,3,5,7,9,11,13,15.....etc
NUMEROS MULTIPLOS,COMPUESTOS Y PRIMOS
MÚLTIPLO DE UN NUMERO: Un numero A es múltiplo de un numero B si al efectuar la división A/B esta es exacta, es decir, el residuo es cero.
EJEMPLOS:
NÚMEROS COMPUESTOS: Es todo numero natural distinto de la unidad y que puede ser expresado como el producto de dos o más enteros positivos diferentes de si mismo, los cuales son sus factores y en algunos casos pueden repetirse.
EJEMPLOS:
4 se puede factorizar en: (2)(2) ó (4)(1).
6 se puede factorizar en: (3)(2) ó (6)(1).
8 se puede factorizar en: (4)(2) ó (8)(1) ó (2)(2)(2).
26 se puede factorizar en: (13)(2) ó (26)(1).
EJEMPLOS:
NÚMEROS COMPUESTOS: Es todo numero natural distinto de la unidad y que puede ser expresado como el producto de dos o más enteros positivos diferentes de si mismo, los cuales son sus factores y en algunos casos pueden repetirse.
EJEMPLOS:
4 se puede factorizar en: (2)(2) ó (4)(1).
6 se puede factorizar en: (3)(2) ó (6)(1).
8 se puede factorizar en: (4)(2) ó (8)(1) ó (2)(2)(2).
26 se puede factorizar en: (13)(2) ó (26)(1).
MINIMO COMUN MULTIPLO
MÍNIMO COMÚN MÚLTIPLO: Un entero es un múltiplo común de dos o mas enteros dados si es múltiplo de cada uno de ellos. Es frecuente tener que usar el menor entero positivo que sea común múltiplo de dos o mas enteros,al cual se le llama mínimo común múltiplo y se simboliza por m.c.m ó M.C.M.
PASOS PARA DETERMINAR EL M.C.M.
1- Se halla la factorización prima de cada número.
2-El M.CM. se forma con el producto de los factores primos comunes y no comunes afectados con su mayor exponente.
EJEMPLOS:
Hallar el m.c.m de 18,24 y 15
PASOS PARA DETERMINAR EL M.C.M.
1- Se halla la factorización prima de cada número.
2-El M.CM. se forma con el producto de los factores primos comunes y no comunes afectados con su mayor exponente.
EJEMPLOS:
Hallar el m.c.m de 18,24 y 15
VALOR ABSOLUTO
VALOR ABSOLUTO: El valor absoluto de x denotado por /x/ indica la magnitud de x sin considerar su signo; existe un valor absoluto dentro de los números el cual es independiente de su posición en la recta así el valor absoluto de un numero cualquiera es la distancia del 0 al numero en cuestión sin tomar en cuenta el sentido positivo o negativo.
Ejemplo:
Ejemplo:
El valor absoluto de todo un numero entero es la distancia que existe entre éste y el cero y se representa como /x/.
ECUACIONES DE SEGUNDO GRADO
ECUACIONES DE SEGUNDO GRADO: Las ecuaciones de segundo grado también se le llama ecuación cuadrática cuando tienen una incógnita X elevado al cuadrado.
EJERCICIOS RESUELTOS
Problema 01:
Solución de la ecuación de segundo grado completa.
Es una ecuación completa con coeficientes a= 4 , b= 4 y c= 1.
ORDINALIDAD Y CARDINALIDAD
NUMERO CARDINAL: Se define como el numero de elementos que contiene un conjunto: su simbolo es #
EJEMPLO:
Conjunto A
El numero de elementos que tiene el conjunto A es 5, por lo que la Cardinalidad del conjunto A es 5
CONJUNTO ORDENADO: Es el conjunto en el cual sus elementos conservan un orden de continuidad.
NUMERO ORDINAL: Se define como el numero natural que sirve para designar cada elemento de un conjunto ordenado.
EJEMPLO:
Conjunto A
El numero de elementos que tiene el conjunto A es 5, por lo que la Cardinalidad del conjunto A es 5
CONJUNTO ORDENADO: Es el conjunto en el cual sus elementos conservan un orden de continuidad.
NUMERO ORDINAL: Se define como el numero natural que sirve para designar cada elemento de un conjunto ordenado.
CLASES DE NUMEROS
CLASES DE NÚMEROS: Los conocimientos de las matemáticas han tenido una influencia determinante en las ciencias naturales, exactas, sociales económicas administrativas y en los avances científicos y tecnológicos; cuando el ser humano se hizo sedentario surgió la necesidad de contar sus bienes (pieles, flechas sus cosechas etc).
Para simbolizar alguna cosa utilizo PIEDRITAS O RAYITAS, para simbolizar alguna cosa u objeto de su propiedad.
En el desarrollo de las culturas fue evolucionando esta forma primitiva de representar objetos o cosas reales a través de símbolos,naciendo así el primer conjunto de números llamados NÚMEROS NATURALES ,estos números son los utilizados para contar,se representan mediante "N" y consta de los siguientes elementos:
Para simbolizar alguna cosa utilizo PIEDRITAS O RAYITAS, para simbolizar alguna cosa u objeto de su propiedad.
En el desarrollo de las culturas fue evolucionando esta forma primitiva de representar objetos o cosas reales a través de símbolos,naciendo así el primer conjunto de números llamados NÚMEROS NATURALES ,estos números son los utilizados para contar,se representan mediante "N" y consta de los siguientes elementos:
FACTORIZACION
FACTORIZACION: La factorización es un proceso contrario a la multiplicación,es decir,el producto se puede descomponer en factores.
FACTOR: Es cada uno de los elementos que al multiplicarse entre si dan lugar a un producto.
FACTORES DE UN MONOMIO: Se determina al descomponer el monomio en factores mas simples.
EJEMPLOS:
FACTOR: Es cada uno de los elementos que al multiplicarse entre si dan lugar a un producto.
FACTORES DE UN MONOMIO: Se determina al descomponer el monomio en factores mas simples.
EJEMPLOS:
PRODUCTOS NOTABLES
PRODUCTOS NOTABLES: Los productos notables cumplen ciertas reglas cuyo resultado puede ser escrito por inspección es decir sin verificar la multiplicación, cada producto notables tiene su formula de factorización.
También los productos notables son aquellos productos que se resuelven con la ayuda de reglas y evitan efectuar todo el producto.
BINOMIO AL CUADRADO: Al elevar un binomio al cuadrado se obtiene un trinomio cuadrado perfecto.
Regla:
° Se eleva al cuadrado el primer termino del binomio.
° Se suma o resta el doble producto del primer termino por el segundo termino del binomio.
° Se suma el cuadrado del segundo termino del binomio.
Ejemplo:
También los productos notables son aquellos productos que se resuelven con la ayuda de reglas y evitan efectuar todo el producto.
BINOMIO AL CUADRADO: Al elevar un binomio al cuadrado se obtiene un trinomio cuadrado perfecto.
Regla:
° Se eleva al cuadrado el primer termino del binomio.
° Se suma o resta el doble producto del primer termino por el segundo termino del binomio.
° Se suma el cuadrado del segundo termino del binomio.
Ejemplo:
OPERACIONES FUNDAMENTALES
OPERACIONES FUNDAMENTALES:
La adición,sustracción,multiplicación y división se llaman operaciones fundamentales del álgebra.
SUMA Y RESTA DE POLINOMIOS
SUMA O ADICIÓN: operación que consiste en reunir dos o mas expresiones algebraicas en una sola.
Para efectuar adiciones con polinomios, se realiza sumando solo términos semejantes.
Ejemplo:
La adición,sustracción,multiplicación y división se llaman operaciones fundamentales del álgebra.
SUMA Y RESTA DE POLINOMIOS
SUMA O ADICIÓN: operación que consiste en reunir dos o mas expresiones algebraicas en una sola.
Para efectuar adiciones con polinomios, se realiza sumando solo términos semejantes.
Ejemplo:
NOTACION ALGEBRAICA
NOTACIÓN ALGEBRAICA: Al estudiar el lenguaje algebraico observamos la aplicación de letras y números,ahora estudiaremos otros elementos que son básicos en la notación algebraica, los cuales se denominan "signos del álgebra";cuya clasificación es:
SIGNOS DEL ÁLGEBRA
1-SIGNOS DE OPERACIÓN:
En álgebra, las operaciones de adición,sustracción,multiplicación,división,potenciacion y radicacion se efectúan en forma similar que en la aritmética.
3-SIGNOS DE AGRUPACIÓN: Se representan normalmente por:
a)Paréntesis curvo
b)Paréntesis recto o corchete
c)Paréntesis de llave
d)Signo de vinculo
SIGNOS DEL ÁLGEBRA
1-SIGNOS DE OPERACIÓN:
En álgebra, las operaciones de adición,sustracción,multiplicación,división,potenciacion y radicacion se efectúan en forma similar que en la aritmética.
Normalmente se colocan entre parentesis los factores:
Ejemplo:
(m) (n)
2-SIGNOS DE RELACIÓN: Los signos que nos permiten identificar la relacion en el que se encuentran dos cantidades.
3-SIGNOS DE AGRUPACIÓN: Se representan normalmente por:
a)Paréntesis curvo
b)Paréntesis recto o corchete
c)Paréntesis de llave
d)Signo de vinculo
DEFINICION DE MATRIZ INVERSA O INVERTIBLE
MATRIZ INVERSA: En algebra lineal, una matriz cuadrada n por n se llama invertible si existe una matriz cuadrada n por n tal que donde Iₙ denota la matriz de identidad n por n y la multiplicacion utilizada es la multiplicacion de matriz ordinaria.
Ejemplo:
Ejemplo:
DEFINICION DE MATRIZ SIMETRICA (2022)
MATRIZ SIMETRICA: Una matriz es simetrica si es una matriz cuadrada, la cual tiene las caracteristicas de ser igual a su traspuesta.
Ejemplo:
Ejemplo:
DEFINICION DE REGLA DE CRAMER
REGLA DE CRAMER: Es un teorema del álgebra lineal que da la solución de un sistema lineal de ecuaciones en términos de determinantes.
Ejemplo:
Ejemplo:
viernes, 27 de febrero de 2015
DEFINICION DE NUMERO ENTERO
NUMERO ENTERO: Un numero entero es un elemento del conjunto numerico que contiene los numeros naturales, sus opuestos y el cero.
Al efectuar la union del conjunto que contiene cero con el conjunto N de los numeros naturales, obtenemos el conjunto de los "NUMEROS ENTEROS POSITIVOS".
Al efectuar la union del conjunto que contiene cero con el conjunto N de los numeros naturales, obtenemos el conjunto de los "NUMEROS ENTEROS POSITIVOS".
Al incluir un elemento aditivo inverso por cada numero natural, obtenemos el conjunto de los "NÚMEROS ENTEROS NEGATIVOS".
La unión del conjunto W con I , da como resultado el conjunto de los "NUMEROS ENTEROS", denotados por:
lunes, 23 de febrero de 2015
DEFINICION DE DIVISIBILIDAD
DIVISIBILIDAD: Es un numero entero b es divisible por otro entero asi existe un entero c tal que esto es equivalente a decir que el resto de la division euclidea es cero.
Ejemplo:
Ejemplo:
DEFINICION DE NUMERO NATURAL
NUMERO NATURAL: Los numeros naturales son aquellos que permiten contar los elementos de un conjunto.
Ejemplo:
1(uno) 2( dos) 3(tres) 4(cuatro) 5(cinco)
Ejemplo:
1(uno) 2( dos) 3(tres) 4(cuatro) 5(cinco)
sábado, 3 de enero de 2015
DEFINICION DE SISTEMA DE ECUACIONES
SISTEMA DE ECUACIONES:Es un sistema de ecuaciones algebraicas ó un conjunto de dos o más ecuaciones con más de una incógnita que conforman un problema matemático que consiste en encontrar los valores de las incógnitas que satisfacen dichas operaciones.
Ejemplo:
Ejemplo:
viernes, 2 de enero de 2015
DEFINICION DE ECUACION DE PRIMER GRADO (2022) Ejemplos
ECUACION DE PRIMER GRADO: Llamada tambien ecuacion lineal es una igualdad que involucra una o más variables a la primera potencia y no contiene productos entre las variables, es decir, una ecuación que involucra solamente sumas y restas de una variable a la primera potencia.
Ejemplo de ecuacion de primer grado y sus partes
EJERCICIOS RESUELTOS:
Solución de ecuación de primer grado con una incógnita:
Ejemplo de ecuacion de primer grado y sus partes
EJERCICIOS RESUELTOS:
Solución de ecuación de primer grado con una incógnita:
jueves, 1 de enero de 2015
POLINOMIO
POLINOMIO: Son aquellos que constan más de un termino, es decir , es la suma algebraica de dos o más monomios.
Ejemplo de polinomio y sus partes
Ejemplo de polinomio y sus partes
Los polinomios de acuerdo al numero de términos puede ser:
a) BINOMIO: polinomio de dos términos
Ejemplo:
b)TRINOMIO: polinomio de tres términos
Ejemplo:
GRADO DE POLINOMIO: El grado del polinomio puede ser "absoluto" y "relativo" a una literal.
GRADO ABSOLUTO: El grado absoluto de un polinomio se determina por el exponente mayor, de uno de sus términos.
Ejemplo:
GRADO RELATIVO A UNA LITERAL: El grado relativo de un polinomio con respecto a una literal, es el mayor exponente que tiene la literal que se considere del polinomio.
EVALUACION DE EXPRESIONES ALGEBRAICAS: Proceso que consiste en sustituir valores numéricos asignados para las literales de una expresión algebraica y que al efectuar las operaciones indicadas se obtiene la evaluación correspondiente.
Suscribirse a:
Entradas (Atom)





































