La probabilidad que un hombre casado vea cierto programa de la televisión, es 40%, la probabilidad que su esposa vea el mismo programa es 50% y la probabilidad que el hombre vea el programa dado que su esposa lo vio es 70%. ¿cual es la probabilidad que al menos uno de los esposos vea el programa?
H --> el hombre ve el programa
M --> la mujer ve el programa.
P(H)=0.40
P(M)=0.50
P(H|M)=0.70 --> P(H|M)=P(H y M)/P(M) --> P(H y M) = P(H|M)*P(M) = 0.70*0.50 = 0.35
Debemos calcular la probabilidad que al menos uno de los esposos vea el programa:
P(H o M) =P(H) + P(M) - P(H y M) = 0.40 + 0.50 - 0.35 = 0.55
Mostrando entradas con la etiqueta TEOREMA DE BAYES. Mostrar todas las entradas
Mostrando entradas con la etiqueta TEOREMA DE BAYES. Mostrar todas las entradas
sábado, 4 de diciembre de 2010
lunes, 24 de mayo de 2010
TEOREMA DE BAYES
1- en cierta cuidad el 40% de la poblacion tiene cabello castaño, el 25% tiene ojos castaños y el 15% tien los ojos y cabello castaño. si se escoje una persona al asar calcular :
a) si tiene cabello castaño, cual es la probabilidad q tambien tenga ojos castaños
b) si tien ojos castaños, cual es la pobabilidad de q tenga cabello castaño
c) cual es la probabilidad de q tenga cabellos y ojos castaños.
Eventos:
C --> Cabello castaño
O --> Ojos castaños.
Nos dicen que:
P(C)=0.40
P(O)=0.25
P(C∩O) = 0.15
a)
Nos piden P(O|C)
P(O|C) = P(C∩O) / P(C) = 0.15/0.40 = 0.375
b)
Nos piden P(C|O) =
P(C|O) = P(C∩O) / P(O) = 0.15/0.25 = 0.6
c)
P(C∩O)= 0.15 según el enunciado.
a) si tiene cabello castaño, cual es la probabilidad q tambien tenga ojos castaños
b) si tien ojos castaños, cual es la pobabilidad de q tenga cabello castaño
c) cual es la probabilidad de q tenga cabellos y ojos castaños.
Eventos:
C --> Cabello castaño
O --> Ojos castaños.
Nos dicen que:
P(C)=0.40
P(O)=0.25
P(C∩O) = 0.15
a)
Nos piden P(O|C)
P(O|C) = P(C∩O) / P(C) = 0.15/0.40 = 0.375
b)
Nos piden P(C|O) =
P(C|O) = P(C∩O) / P(O) = 0.15/0.25 = 0.6
c)
P(C∩O)= 0.15 según el enunciado.
TEOREMA DE BAYES
1- Los estudios epidemiológicos indican que el 20% de los ancianos sufren un deterioro neuropsicológico. Sabemos que la tomografía axial computerizada (TAC) es capaz de detectar este trastorno en el 80% de los que lo sufren, pero que también da un 3% de falsos positivos entre personas sanas. Si tomamos un anciano al azar y da positivo en el TAC, ¿cuál es la probabilidad de que esté realmente enfermo?
Eventos:
D --> Sufrir deterioro --> D' Estar sano
T --> Trastorno detectado
Nos dicen que
P(D)=0.20 --> P(D') = 0.80
P(T|D)=0.80
P(T|D') = 0.03
Nos piden calcular P(D|T) :
Por el teorema de Bayes:
P(D|T) = P(T|D)*P(D) / { P(T|D)*P(D) + P(T|D')*P(D') }
P(D|T) = 0.80*0.20 / { 0.80*0.20 + 0.03*0.80 }
P(D|T) = 0.8696
Eventos:
D --> Sufrir deterioro --> D' Estar sano
T --> Trastorno detectado
Nos dicen que
P(D)=0.20 --> P(D') = 0.80
P(T|D)=0.80
P(T|D') = 0.03
Nos piden calcular P(D|T) :
Por el teorema de Bayes:
P(D|T) = P(T|D)*P(D) / { P(T|D)*P(D) + P(T|D')*P(D') }
P(D|T) = 0.80*0.20 / { 0.80*0.20 + 0.03*0.80 }
P(D|T) = 0.8696
lunes, 17 de mayo de 2010
TEOREMA DE BAYES (2022) Ejemplos
😁
TEOREMA DE BAYES: Es una preposicion planteada que expresa la probabilidad condicional de un evento aleatorio A dado B en terminos de la distribucion de probabilidad condicional del evento B dado A .
EJERCICIOS RESUELTOS
Problema 1
Dos maquina producen cada una la mitad de tornillos que produce la fabrica, la maquina A produce el 15 % de tornillos defectuosos y la B produce el 25%
Si la maquina C elige un tornillo al azar y resulta defectuoso ¿cual es la probabilidad de que:
a) Venga de la Maquina A
b) Venga de la Maquina B
Sucesos:
A: Tornillo producido por la maquina A
B: Tornillo producido por la maquina B
Como cada una produce la mitad de tornillos
=P(B)=0.5)
D: Tornillo defectuoso Nos dice que:
=0.15\rightarrow) El 15 % de los tornillos de A son defectuosos
El 15 % de los tornillos de A son defectuosos
=0.25\rightarrow) El 25 % de los tornillos de B son defectuosos
El 25 % de los tornillos de B son defectuosos
Solución Inciso a)
Nos piden calcular) la probabilidad que si el tornillo es defectuoso
la probabilidad que si el tornillo es defectuoso ) venga de la maquina A.
venga de la maquina A.
Por el Teorema de Bayes
=\frac{P(D/A)\ast&space;P(A)}{\left&space;\{&space;P(D/A\ast&space;P(A)+&space;P(D/B\ast&space;P(B)&space;\right&space;\}})
=\frac{0.15\ast&space;0.5}{\left&space;\{&space;0.15\ast&space;0.5+&space;0.25\ast&space;0.5&space;\right&space;\}}=\frac{3}{8}=0.375)
Solucion Inciso b)
Nos piden calcular) la probabilidad que si el tornillo es defectuoso
la probabilidad que si el tornillo es defectuoso ) venga de la maquina B.
venga de la maquina B.
Por el Teorema de Bayes
=\frac{P(D/B)\ast&space;P(B)}{\left&space;\{P(D/A)\ast&space;P(A)+&space;P(D/B)\ast&space;P(B)&space;\right&space;\}})
=\frac{0.25\ast&space;0.5}{\left&space;\{&space;0.15\ast&space;0.5+&space;0.25\ast&space;0.5&space;\right&space;\}}=\frac{5}{8}=0.625)
Problema 2
Se recibieron dos cajas de camisas para hombre provenientes de la fabrica, La caja 1 contenia 25 camisas deportivas y 15 de vestir y la caja 2 30 deportivas y 10 de vestir . Se eligio a azar una caja y se selecciono aleatoriamente una camisa de esa caja para inspeccionarla y la camisa resulto ser deportiva ¿ Cual es la probabilidad de que la caja de la que proviene la camisa sea la caja uno?
Solución Inciso a)

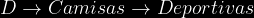
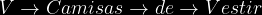
)
)
La probabilidad de escoger cualquier caja es:
=\frac{1}{2}=0.5)
=\frac{1}{2}=0.5)
Segun el enunciado la probabilidad de cada tipo de camisa en cada caja es:
=\frac{25}{25+15}=\frac{25}{40}=0.625)
=\frac{15}{25+15}=\frac{15}{40}=0.375)
=\frac{30}{30+10}=\frac{30}{40}=0.75)
=\frac{10}{30+10}=\frac{10}{40}=0.25)
Nos piden calcular cual es la probabilidad de que la caja de la que proviene la camisa sea la caja uno si ha salido una camisa deportiva es decir,
)
Utilizando el Teorema de Bayes
=\frac{P(D/C1)\ast&space;P(C1)}{\left&space;\{P(D/C1)\ast&space;P(C1)+&space;P(D/C2)\ast&space;P(C2)&space;\right&space;\}})
=\frac{0.625\ast&space;0.5}{\left&space;\{&space;0.625\ast&space;0.5+&space;0.75\ast&space;0.5&space;\right&space;\}}=)
=0.4545)
La probabilidad buscada es de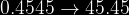 %
%
EJERCICIOS RESUELTOS
Problema 1
Dos maquina producen cada una la mitad de tornillos que produce la fabrica, la maquina A produce el 15 % de tornillos defectuosos y la B produce el 25%
Si la maquina C elige un tornillo al azar y resulta defectuoso ¿cual es la probabilidad de que:
a) Venga de la Maquina A
b) Venga de la Maquina B
Sucesos:
A: Tornillo producido por la maquina A
B: Tornillo producido por la maquina B
Como cada una produce la mitad de tornillos
D: Tornillo defectuoso Nos dice que:
Solución Inciso a)
Nos piden calcular
Por el Teorema de Bayes
Solucion Inciso b)
Nos piden calcular
Por el Teorema de Bayes
Problema 2
Se recibieron dos cajas de camisas para hombre provenientes de la fabrica, La caja 1 contenia 25 camisas deportivas y 15 de vestir y la caja 2 30 deportivas y 10 de vestir . Se eligio a azar una caja y se selecciono aleatoriamente una camisa de esa caja para inspeccionarla y la camisa resulto ser deportiva ¿ Cual es la probabilidad de que la caja de la que proviene la camisa sea la caja uno?
Solución Inciso a)
La probabilidad de escoger cualquier caja es:
Segun el enunciado la probabilidad de cada tipo de camisa en cada caja es:
Nos piden calcular cual es la probabilidad de que la caja de la que proviene la camisa sea la caja uno si ha salido una camisa deportiva es decir,
Utilizando el Teorema de Bayes
La probabilidad buscada es de
TEOREMA DE BAYES
-el 5% de la produccion de sacos de café es rechazada cuando el cultivo tiene la plaga controlada. Si la plaga se sale de control, el 30% de la produccion de sacos de café es rechazada. La probabilidad marginal que la plaga este controlada es 0.92. Si se escoge un saco aleatoriamente y se sabe que va a ser rechazado ¿Cúal es la probabilidad que el cultivo tenga controlada la plaga?
Sucesos :
R --> Saco rechazado
P --> Plaga controlada : P' --> Plaga no controlada
Nos dicen que
P(R|P) = 0.05
P(R|P') = 0.30
P(P) = 0.92 --> P(P') = 1-0.92 = 0.08
Nos piden
P(P|R)
Por el teorema de Bayes
P(P|R) = P(R|P)*P(P) / ( P(R|P)*P(P) + P(R|P')*P(P')
P(P|R) = 0.05*0.92 / ( 0.05*0.92 + 0.30*0,08)
P(P|R) = 0.6571
La probabilidad buscada es 0.6571
Sucesos :
R --> Saco rechazado
P --> Plaga controlada : P' --> Plaga no controlada
Nos dicen que
P(R|P) = 0.05
P(R|P') = 0.30
P(P) = 0.92 --> P(P') = 1-0.92 = 0.08
Nos piden
P(P|R)
Por el teorema de Bayes
P(P|R) = P(R|P)*P(P) / ( P(R|P)*P(P) + P(R|P')*P(P')
P(P|R) = 0.05*0.92 / ( 0.05*0.92 + 0.30*0,08)
P(P|R) = 0.6571
La probabilidad buscada es 0.6571
Suscribirse a:
Comentarios (Atom)
