TEOREMA DE BAYES: Es una preposicion planteada que expresa la probabilidad condicional de un evento aleatorio A dado B en terminos de la distribucion de probabilidad condicional del evento B dado A .
EJERCICIOS RESUELTOS
Problema 1
Dos maquina producen cada una la mitad de tornillos que produce la fabrica, la maquina A produce el 15 % de tornillos defectuosos y la B produce el 25%
Si la maquina C elige un tornillo al azar y resulta defectuoso ¿cual es la probabilidad de que:
a) Venga de la Maquina A
b) Venga de la Maquina B
Sucesos:
A: Tornillo producido por la maquina A
B: Tornillo producido por la maquina B
Como cada una produce la mitad de tornillos
=P(B)=0.5 "P(A)=P(B)=0.5")
D: Tornillo defectuoso Nos dice que:
=0.15\rightarrow "P(D/A)=0.15\rightarrow")
El 15 % de los tornillos de A son defectuosos
=0.25\rightarrow "P(D/B)=0.25\rightarrow")
El 25 % de los tornillos de B son defectuosos
Solución Inciso a)
Nos piden calcular "P(A/D)")
la probabilidad que si el tornillo es defectuoso  "(D)")
venga de la maquina A.
Por el Teorema de Bayes
=\frac{P(D/A)\ast&space;P(A)}{\left&space;\{&space;P(D/A\ast&space;P(A)+&space;P(D/B\ast&space;P(B)&space;\right&space;\}} "\bg_black P(A/D)=\frac{P(D/A)\ast P(A)}{\left \{ P(D/A\ast P(A)+ P(D/B\ast P(B) \right \}}")
=\frac{0.15\ast&space;0.5}{\left&space;\{&space;0.15\ast&space;0.5+&space;0.25\ast&space;0.5&space;\right&space;\}}=\frac{3}{8}=0.375 "\bg_black P(A/D)=\frac{0.15\ast 0.5}{\left \{ 0.15\ast 0.5+ 0.25\ast 0.5 \right \}}=\frac{3}{8}=0.375")
Solucion Inciso b)
Nos piden calcular "P(B/D)")
la probabilidad que si el tornillo es defectuoso venga de la maquina B.
Por el Teorema de Bayes
=\frac{P(D/B)\ast&space;P(B)}{\left&space;\{P(D/A)\ast&space;P(A)+&space;P(D/B)\ast&space;P(B)&space;\right&space;\}} "\bg_black P(B/D)=\frac{P(D/B)\ast P(B)}{\left \{P(D/A)\ast P(A)+ P(D/B)\ast P(B) \right \}}")
=\frac{0.25\ast&space;0.5}{\left&space;\{&space;0.15\ast&space;0.5+&space;0.25\ast&space;0.5&space;\right&space;\}}=\frac{5}{8}=0.625 "\bg_black P(A/D)=\frac{0.25\ast 0.5}{\left \{ 0.15\ast 0.5+ 0.25\ast 0.5 \right \}}=\frac{5}{8}=0.625")
Problema 2
Se recibieron dos cajas de camisas para hombre provenientes de la fabrica, La caja 1 contenia 25 camisas deportivas y 15 de vestir y la caja 2 30 deportivas y 10 de vestir . Se eligio a azar una caja y se selecciono aleatoriamente una camisa de esa caja para inspeccionarla y la camisa resulto ser deportiva ¿ Cual es la probabilidad de que la caja de la que proviene la camisa sea la caja uno?
Solución Inciso a)
 "C1\rightarrow Caja(1)")
 "C2\rightarrow Caja(2)")
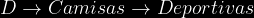
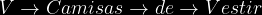
La probabilidad de escoger cualquier caja es:
=\frac{1}{2}=0.5 "P(C1)=\frac{1}{2}=0.5")
=\frac{1}{2}=0.5 "P(C2)=\frac{1}{2}=0.5")
Segun el enunciado la probabilidad de cada tipo de camisa en cada caja es:
=\frac{25}{25+15}=\frac{25}{40}=0.625 "P(D/C1)=\frac{25}{25+15}=\frac{25}{40}=0.625")
=\frac{15}{25+15}=\frac{15}{40}=0.375 "P(V/C1)=\frac{15}{25+15}=\frac{15}{40}=0.375")
=\frac{30}{30+10}=\frac{30}{40}=0.75 "P(D/C2)=\frac{30}{30+10}=\frac{30}{40}=0.75")
=\frac{10}{30+10}=\frac{10}{40}=0.25 "P(V/C2)=\frac{10}{30+10}=\frac{10}{40}=0.25")
Nos piden calcular cual es la probabilidad de que la caja de la que proviene la camisa sea la caja uno si ha salido una camisa deportiva es decir,
 "P(C1/D)")
Utilizando el Teorema de Bayes
=\frac{P(D/C1)\ast&space;P(C1)}{\left&space;\{P(D/C1)\ast&space;P(C1)+&space;P(D/C2)\ast&space;P(C2)&space;\right&space;\}} "\bg_black P(C1/D)=\frac{P(D/C1)\ast P(C1)}{\left \{P(D/C1)\ast P(C1)+ P(D/C2)\ast P(C2) \right \}}")
=\frac{0.625\ast&space;0.5}{\left&space;\{&space;0.625\ast&space;0.5+&space;0.75\ast&space;0.5&space;\right&space;\}}= "\bg_black P(C1/D)=\frac{0.625\ast 0.5}{\left \{ 0.625\ast 0.5+ 0.75\ast 0.5 \right \}}=")
=0.4545 "P(C1/D)=0.4545")
La probabilidad buscada es de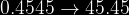
%
EJERCICIOS RESUELTOS
Problema 1
Dos maquina producen cada una la mitad de tornillos que produce la fabrica, la maquina A produce el 15 % de tornillos defectuosos y la B produce el 25%
Si la maquina C elige un tornillo al azar y resulta defectuoso ¿cual es la probabilidad de que:
a) Venga de la Maquina A
b) Venga de la Maquina B
Sucesos:
A: Tornillo producido por la maquina A
B: Tornillo producido por la maquina B
Como cada una produce la mitad de tornillos
D: Tornillo defectuoso Nos dice que:
Solución Inciso a)
Nos piden calcular
Por el Teorema de Bayes
Solucion Inciso b)
Nos piden calcular
Por el Teorema de Bayes
Problema 2
Se recibieron dos cajas de camisas para hombre provenientes de la fabrica, La caja 1 contenia 25 camisas deportivas y 15 de vestir y la caja 2 30 deportivas y 10 de vestir . Se eligio a azar una caja y se selecciono aleatoriamente una camisa de esa caja para inspeccionarla y la camisa resulto ser deportiva ¿ Cual es la probabilidad de que la caja de la que proviene la camisa sea la caja uno?
Solución Inciso a)
La probabilidad de escoger cualquier caja es:
Segun el enunciado la probabilidad de cada tipo de camisa en cada caja es:
Nos piden calcular cual es la probabilidad de que la caja de la que proviene la camisa sea la caja uno si ha salido una camisa deportiva es decir,
Utilizando el Teorema de Bayes
La probabilidad buscada es de
