👉DISTRIBUCION GEOMETRICA:
La distribución geométrica se relaciona también con una secuencia de ensayos de Bernoulli con la diferencia de que el numero de ensayos no es fijo y, de hecho, la variable aleatoria de interés,denotada por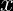 , se define como el numero de ensayos requeridos para alcanzar el primer éxito.
, se define como el numero de ensayos requeridos para alcanzar el primer éxito.
El espacio del rango para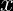 es
es 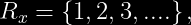 y la distribución de
y la distribución de 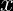 esta dada por:
esta dada por:
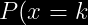=q^{k-1}p)
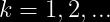
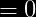 en otro caso
en otro caso
=\frac{1}{p&space;})
DESVIACIÓN ESTÁNDAR LLAMADA TAMBIÉN VARIANZA
=\frac{1-p}{p^{2}&space;})
Un Experimento aleatorio se llama geométrico, si cumple con:
1- El experimento consta de ensayos independientes.
2- Cada ensayo tiene sólo dos resultados. Éxito y Fracaso.
3- La probabilidad de éxito en un ensayo es p y la de fracaso q=1-p, y se mantienen constantes de ensayo en ensayo.
4- El experimento termina cuando ocurre el primer éxito en un ensayo.
DISTRIBUCION GEOMETRICA EN LA VIDA COTIDIANA
q=1-p, entonces:
👉 Problema 01: 😆
👉 Problema 02: 😆
Tres personas tiran una moneda al aire y el disparejo pagara los refrescos. Si los tres resultados son iguales, las monedas se tiran nuevamente hasta que resulte el primer perdedor.
a) encuentre la probabilidad de que se necesiten menos de 4 intentos para determinar el perdedor.
b) ¿en cuántos intentos se espera obtener al perdedor?
Lanzamientos posibles
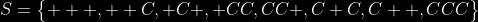
En cada lanzamiento hay una probabilidad de
=\frac{6}{8}=\frac{3}{4})
=\frac{2}{8}=\frac{1}{4})
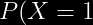=\frac{3}{4})
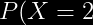=\left&space;(&space;\frac{3}{4}&space;\right&space;)\left&space;(&space;\frac{1}{4}&space;\right&space;)=\frac{3}{16})
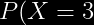=\left&space;(&space;\frac{3}{4}&space;\right&space;)\left&space;(&space;\frac{1}{4}&space;\right&space;)^{2}=\frac{3}{64})
=P(X=1)+P(X=2)+P(X=3))
=\frac{3}{4}+\frac{3}{16}+\frac{3}{64}=\frac{63}{64})
=0.9844)
👉 Problema 03: 😆
Si el 25% de la población del DF, esta a favor del candidato Roberto Madrazo para las elecciones del 2006.
a)Encuentre la probabilidad que la primera persona que este a favor del candidato Madrazo, se encuentre después de la quinta persona entrevistada,
b)¿Cuantas personas se espera entrevistar hasta encontrar la primera que este a favor del candidato Madrazo?
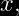 "Cantidad de personas que se va entrevistar aleatoriamente hasta obtener la primera que este a favor del candidato Roberto Madrazo"
"Cantidad de personas que se va entrevistar aleatoriamente hasta obtener la primera que este a favor del candidato Roberto Madrazo"
Clasificaremos el modelo resultando que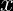 cumple con una variable geométrica con:
cumple con una variable geométrica con:
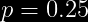
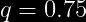
Finalmente Utilizamos la Aplicación de Formulas:
Formula:
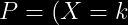=q^{k-1}p)
=1-P(x\leq&space;5))
Donde:
=P(X=1)+P(X=2)+P(X=3)+P(X=4)+P(X=5))
Sustituimos en la Formula General:
(0.25)+(0.75^{2-1})(0.25)+(0.75^{3-1})(0.25)&space;+\right)
![\left [ (0.75^{4-1})(0.25)+(0.75^{5-1})(0.25) \right ]=0.7627](https://latex.codecogs.com/png.latex?\dpi{120}&space;\bg_black&space;\left&space;[&space;(0.75^{4-1})(0.25)+(0.75^{5-1})(0.25)&space;\right&space;]=0.7627)
Por lo tanto:
=1-0.7627=0.2373)
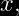 "Cantidad de personas que se va entrevistar aleatoriamente hasta obtener al primer consumidor que prefiera la marca A"
"Cantidad de personas que se va entrevistar aleatoriamente hasta obtener al primer consumidor que prefiera la marca A"
Finalmente Utilizamos la Aplicación de Formulas:
Formula:
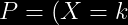=q^{k-1}p)
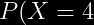=&space;(0.30^{4-1})(0.70)=0.0189)
Formula:
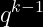
Sustituyendo los valores en la formula:
=(0.30)^{6-1}=0.00243)
Finalmente Utilizamos la Aplicación de Formulas:
Formula:
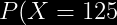=&space;(0.99^{125-1})(0.01)=0.0029)
Finalmente Utilizamos la Aplicación de Formulas:
Formula:
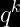
Sustituyendo los valores en la formula:
=(0.95)^{15}=0.4632)
Solución Inciso b)
=\frac{1}{p&space;}=\frac{1}{0.05}=20)
La distribución geométrica se relaciona también con una secuencia de ensayos de Bernoulli con la diferencia de que el numero de ensayos no es fijo y, de hecho, la variable aleatoria de interés,denotada por
El espacio del rango para
ESPERANZA MATEMÁTICA LLAMADO TAMBIÉN VALOR ESPERADO
DESVIACIÓN ESTÁNDAR LLAMADA TAMBIÉN VARIANZA
Un Experimento aleatorio se llama geométrico, si cumple con:
1- El experimento consta de ensayos independientes.
2- Cada ensayo tiene sólo dos resultados. Éxito y Fracaso.
3- La probabilidad de éxito en un ensayo es p y la de fracaso q=1-p, y se mantienen constantes de ensayo en ensayo.
4- El experimento termina cuando ocurre el primer éxito en un ensayo.
DISTRIBUCION GEOMETRICA EN LA VIDA COTIDIANA
Definición de Variable aleatoria Geométrica:
A la variable aleatoria discreta X definida en un experimento geométrico que representa a la cantidad de pruebas necesarias hasta obtener el primer éxito se le llama Variable aleatoria Geométrica.
Ejemplo:
1- Al lanzar una moneda perfecta se puede definir a la variable aleatoria:
X:"cantidad de lanzamientos hasta que resulte la primera águila"
2- Si el 35% de la población, del DF., esta a favor del candidato cuauhtemoc cárdenas, para las elecciones del 2000, podemos definir a la variable aleatoria:
X:"Cantidad de personas que se va a entrevistar aleatoriamente hasta obtener la primera que este en favor del candidato."
3- Si una maquina despachadora de refrescos arroja un poco mas de 200 ml. por vaso derramándose el liquido en un 5%, de los vasos despachados. Podemos definir a la variable aleatoria:
X:"Cantidad de vasos despachados, hasta obtener el primero que se derramara"
Simbolizaremos por G(k;p)= p=(x=k) a la probabilidad de que el primer exito ocurra en el ensayo k. La formula para calcular las probabilidades de un Modelo Geometrico estara dada por el siguiente teorema:
Si x es una variable aleatoria geométrica, con éxito p y fracaso
q=1-p, entonces:
EJERCICIOS RESUELTOS
👉 Problema 01: 😆
Se va realizar cierto experimento hasta que se obtenga un resultado exitoso. Los ensayos son independientes y el costo de efectuar el experimento es de $ 25,000 dolares; sin embargo,si se produce una falla, cuesta $5,000 dolares "iniciar"el siguiente ensayo. Al experimentador le gustaria determinar el costo esperado del proyecto. Si 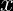 es el numero de ensayos que se requieren para obtener un experimento exitoso, entonces la funcion del costo seria.
es el numero de ensayos que se requieren para obtener un experimento exitoso, entonces la funcion del costo seria.
Solución Inciso a)
=\$&space;25,000X+\$&space;5,000(X-1))
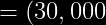X+(-5000))
En consecuencia:
![=E\left [ C(X) \right ]=\$ 30,000\cdot E(X)-E(\$ 5,000)](https://latex.codecogs.com/png.latex?\dpi{120}&space;\bg_black&space;=E\left&space;[&space;C(X)&space;\right&space;]=\$&space;30,000\cdot&space;E(X)-E(\$&space;5,000))
![=\left [ 30,000\cdot \frac{1}{P} \right ]-5000](https://latex.codecogs.com/png.latex?\dpi{120}&space;\bg_black&space;=\left&space;[&space;30,000\cdot&space;\frac{1}{P}&space;\right&space;]-5000)
Si la probabilidad del exito en un solo ensayo es, por ejemplo, .25, entonces la
![E\left [ C(X) \right ]=\$ 30,000/.25-\$ 5,000=\$ 115,000.](https://latex.codecogs.com/png.latex?\dpi{120}&space;\bg_black&space;E\left&space;[&space;C(X)&space;\right&space;]=\$&space;30,000/.25-\$&space;5,000=\$&space;115,000.)
Este puede ser o no aceptable para el experimentador. Debe tambien reconocerse que es posible continuar indefinidamente sin que se logre un experimento exitoso. Supongase que el experimentador tiene un maximo de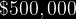 . Puede desear obtener la probabilidad de que el trabajo experimental costaria mas de esta cantidad, esto es,
. Puede desear obtener la probabilidad de que el trabajo experimental costaria mas de esta cantidad, esto es,
>&space;\$&space;500,000))
)
)
)
)
^{x-1})
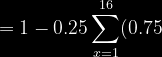^{x-1})
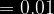
En consecuencia:
Si la probabilidad del exito en un solo ensayo es, por ejemplo, .25, entonces la
Este puede ser o no aceptable para el experimentador. Debe tambien reconocerse que es posible continuar indefinidamente sin que se logre un experimento exitoso. Supongase que el experimentador tiene un maximo de
👉 Problema 02: 😆
Tres personas tiran una moneda al aire y el disparejo pagara los refrescos. Si los tres resultados son iguales, las monedas se tiran nuevamente hasta que resulte el primer perdedor.
a) encuentre la probabilidad de que se necesiten menos de 4 intentos para determinar el perdedor.
b) ¿en cuántos intentos se espera obtener al perdedor?
Lanzamientos posibles
En cada lanzamiento hay una probabilidad de
Solución Inciso a)
Solución Inciso b)
La esperanza de la distribución geométrica es:
Si el 25% de la población del DF, esta a favor del candidato Roberto Madrazo para las elecciones del 2006.
a)Encuentre la probabilidad que la primera persona que este a favor del candidato Madrazo, se encuentre después de la quinta persona entrevistada,
b)¿Cuantas personas se espera entrevistar hasta encontrar la primera que este a favor del candidato Madrazo?
Solución Inciso a)
Clasificaremos el modelo resultando que
Finalmente Utilizamos la Aplicación de Formulas:
Formula:
Donde:
Sustituimos en la Formula General:
Por lo tanto:
Solución Inciso b)
En la Formula se sustituyen los valores:
👉 Problema 04: 😆
Se estima que el 70 % de una población de consumidores prefiere una marca en particular de pasta de dientes A ¿cuál es la probabilidad que al entrevistar a un grupo de consumidores.
Se estima que el 70 % de una población de consumidores prefiere una marca en particular de pasta de dientes A ¿cuál es la probabilidad que al entrevistar a un grupo de consumidores.
a) sea necesario entrevistar exactamente 4 personas para encontrar el primer consumidor que prefiere la marca A?
b) Se tenga que entrevistar a lo más 6 personas para encontrar el primer consumidor que prefiere la marca A?
Solución Inciso a)
Finalmente Utilizamos la Aplicación de Formulas:
Formula:
Solución Inciso b)
Formula:
Sustituyendo los valores en la formula:
👉 Problema 05: 😆
La probabilidad de que una muestra de aire contenga una molécula rara es de 0.01 si se supone que las muestras son independientes con respecto a la presencia de la molécula rara.
La probabilidad de que una muestra de aire contenga una molécula rara es de 0.01 si se supone que las muestras son independientes con respecto a la presencia de la molécula rara.
¿Cuál es la probabilidad de que sea necesario analizar exactamente 125 muestras antes de detectar una molécula rara?
Solución Inciso a)
Formula:
👉 Problema 06: 😆
Sea una máquina despachadora de refrescos que arroja un poco más de 20 ml por vaso derramándose el líquido en un 5% de los vasos despachados. Podemos definir la variable aleatoria X: “cantidad de vasos despachados hasta obtener el primero que se derramará” Considere que la forma de despachar el líquido por la máquina es independiente de vaso en vaso.
Sea una máquina despachadora de refrescos que arroja un poco más de 20 ml por vaso derramándose el líquido en un 5% de los vasos despachados. Podemos definir la variable aleatoria X: “cantidad de vasos despachados hasta obtener el primero que se derramará” Considere que la forma de despachar el líquido por la máquina es independiente de vaso en vaso.
a) calcule la probabilidad de que el primer vaso que se derrame se encuentre después del 15vo. Vaso despachado.
b) Qué vaso despachado se espera sea el primero en el que se derrame el líquido.
Solución Inciso a)
Finalmente Utilizamos la Aplicación de Formulas:
Formula:
Sustituyendo los valores en la formula:
Solución Inciso b)
En la Formula se sustituyen los valores:
👉 Problema 07: 😆
Un inspector de la SECOFI ha encontrado que en 6 de 10 tiendas que visita se presentan irregularidades. Si el inspector visita una serie de tiendas al azar ¿Cuál es la probabilidad de que:
Un inspector de la SECOFI ha encontrado que en 6 de 10 tiendas que visita se presentan irregularidades. Si el inspector visita una serie de tiendas al azar ¿Cuál es la probabilidad de que:
a) la primera tienda con irregularidades fuera encontrada después de revisar la cuarta?