lunes, 17 de mayo de 2010
DISTRIBUCION BINOMIAL (2022) Ejemplos
👉 Problema 01:😆
a) La luz roja sale con una frecuencia del 10%, si se consideran 18 viajeros, ¿Cuál es la probabilidad de que más de uno y a lo más 4 sean revisados?
b) Si la luz roja aparece con una frecuencia del 15%, ¿Cuál es la probabilidad de que antes de la cuarta persona que pase en el semáforo, se tenga la primera que va a ser revisada?
Solución Inciso a)
La formula es
En este caso
P(X=x) =C(18,x) * 0.10^x * 0.90^(18-x)
Debemos calcular la probabilidad
P(1<=X<=4) = P(X=1) + P(X=2) + P(X=3) + P(X=4)
P(X=1) =C(18,1) * 0.10^1 * 0.90^(18-1) = 0.3002
P(X=2) =C(18,2) * 0.10^2 * 0.90^(18-2) = 0.2835
P(X=3) =C(18,3) * 0.10^3 * 0.90^(18-3) = 0.1680
P(X=4) =C(18,4) * 0.10^4 * 0.90^(18-4) = 0.0700
P(1<=X<=4) = P(X=1) + P(X=2) + P(X=3) + P(X=4)
P(1<=X<=4) = 0.8217
La función de probabilidad acumulada de la distribución geometrica ( P(X=x) = p(1-p)^(x-1) es
P(X<=n) = 1 - (1-p) ^n
n=4
p=0.15
P(X<=4) = 1 - (1-0.15)^4 = 0.4780
Suponga que una compañía de seguros de vida asegura a 5000 hombres de 42 años de edad. Si los estudios realizados muestran que la probabilidad de que un hombre de 42 años fallezca en un cierto año es de 0.001, calcule la probabilidad de que la compañía pague durante un año dado:
%
2)
p=0.001
n=5000
Debemos calcular la probabilidad P(X>=1), es decir la probabilidad que fallezca algun hombre y la compañía pague. Esta probabilidad es lo contraria a que no pague, es decir que no fallezca ninguno de los 5000 hombres, esta probabilidad es
P(X=0) = (1-p)^n = (1-0.001)^5000 = 0.0067
Por lo tanto la probabilidad que fallezca alguno y la compañía tenga que pagar es
P(X>=1) = 1-P(X=0) = 1-(1-p)^n = 1-0.0067 = 0.9932
P(X=x) =C(18,x) * 0.10^x * 0.90^(18-x)
Debemos calcular la probabilidad
P(1<=X<=4) = P(X=1) + P(X=2) + P(X=3) + P(X=4)
P(X=1) =C(18,1) * 0.10^1 * 0.90^(18-1) = 0.3002
P(X=2) =C(18,2) * 0.10^2 * 0.90^(18-2) = 0.2835
P(X=3) =C(18,3) * 0.10^3 * 0.90^(18-3) = 0.1680
P(X=4) =C(18,4) * 0.10^4 * 0.90^(18-4) = 0.0700
P(1<=X<=4) = P(X=1) + P(X=2) + P(X=3) + P(X=4)
P(1<=X<=4) = 0.8217
Solución Inciso b)
P(X<=n) = 1 - (1-p) ^n
n=4
p=0.15
P(X<=4) = 1 - (1-0.15)^4 = 0.4780
👉 Problema 02:😆
%
2)
p=0.001
n=5000
Debemos calcular la probabilidad P(X>=1), es decir la probabilidad que fallezca algun hombre y la compañía pague. Esta probabilidad es lo contraria a que no pague, es decir que no fallezca ninguno de los 5000 hombres, esta probabilidad es
P(X=0) = (1-p)^n = (1-0.001)^5000 = 0.0067
Por lo tanto la probabilidad que fallezca alguno y la compañía tenga que pagar es
P(X>=1) = 1-P(X=0) = 1-(1-p)^n = 1-0.0067 = 0.9932
INTERVALOS DE CONFIANZA
-Se prueba una muestra aleatoria de 400 componentes electrónicos fabricados por cierto proceso electrónico y se encuentra que 30 están defectuosos.
¿Cuántos componentes se deben muestrear con el propósito de que el intervalo de confianza de 95% especifique la proporción defectuosa dentro de ±0.02?
p=30/400
n>=Z²p(1-p)/d²
95%--> Z=1.96
n>=1.96²30/400*(1-30/400)/0.02²
n>=666.2775
Redondeando a enteros
n>=667
La muestra debe tener 667 componentes o más.
¿Cuántos componentes se deben muestrear con el propósito de que el intervalo de confianza de 95% especifique la proporción defectuosa dentro de ±0.02?
p=30/400
n>=Z²p(1-p)/d²
95%--> Z=1.96
n>=1.96²30/400*(1-30/400)/0.02²
n>=666.2775
Redondeando a enteros
n>=667
La muestra debe tener 667 componentes o más.
Una urna contiene 4 bolas con los números 1, 2, 3 y 4 respectivamente. Si se toman dos bolas de la urna sin sustitución y X representa la suma de los números de las dos bolas extraídas.
Determine la función de probabilidad f(X), el valor esperado E(X) y la varianza de la variable aleatoria
1)
Posibilidades
Bolas --- Suma
1,2 --> 3
1,3 --> 4
1,4 --> 5
2,1 --> 3
2,3 --> 5
2,4 --> 6
3,1 --> 4
3,2 --> 5
3,4 --> 7
4,1 --> 5
4,2 --> 6
4,3 --> 7
Hay 2 posibilidades con suma 3, 2 con suma 4, 4 con suma 5 2 con suma 6 y 2 con suma 7 es decir
X --- frecuencia
3 --- 2
4 --- 2
5 --- 4
6 --- 2
7 --- 2
Tenemos 2+2+4+2+2=12 posibilidades por lo que las probabilidades son
3 --- 2/12 = 1/6
4 --- 2/12 = 1/6
5 --- 4/12 = 1/3
6 --- 2/12 = 1/6
7 --- 2/12 = 1/6
por lo tanto la función de probabilidad es
X -- f(x)
3 --- 1/6
4 --- 1/6
5 --- 1/3
6 --- 1/6
7 --- 1/6
E(x)= suma de x*f(x)
E(x)= 3*1/6 + 4*1/6 + 5*1/3+6*1/6 + 7*1/6
E(X)=5
La varianza es la suma de f(x)*(x-E(X))²
V(X)=1/6*(3-5)² + 1/6*(4-5)² + 1/3*(5-5)² +1/6*(6-5)² + 1/6*(7-5)²
V(X)=5/3
Al invertir en acciones financieras, una persona puede lograr una ganancia de 4000 dólares en un año con probabilidad de 0.3 o bien tener una pérdida de 1.000 dólares con probabilidad de 0.7. Cuál sería la ganancia esperada de esa persona.
2)
X --- p(x)
4000 --- 0.3
-1000 --- 0.7
E(X) = suma x*p(x)
E(X)=4000*0.3+(-1000)*0.7 =
E(X)=500
MEDIA MUESTRAL (2022) Ejemplos
-Suponga que la población de temperaturas corporales humanas tiene una media
de 98,6°F (37°C), como se cree comúnmente. Suponga también que la
desviación estándar de la población es de 0,62°F. Si se escoge aleatoriamente
una muestra de tamaño 106, calcule la probabilidad de obtener una media
menor a 98.2°F.
Media = 98.6
desv = 0.62
n=106
P(X<98 .2="" br="">
Estandarizamos con Z=(X-Media)/(desv/√n)
X=98.2 --> Z=(98.2-98.6)/(0.62/√106) = -6.6423
P(X<98 .2="" 0="" 1.279017="" br="" decir="" es="" p="" practicamente="">
Por lo tanto
P(X
de 98,6°F (37°C), como se cree comúnmente. Suponga también que la
desviación estándar de la población es de 0,62°F. Si se escoge aleatoriamente
una muestra de tamaño 106, calcule la probabilidad de obtener una media
menor a 98.2°F.
Media = 98.6
desv = 0.62
n=106
P(X<98 .2="" br="">
Estandarizamos con Z=(X-Media)/(desv/√n)
X=98.2 --> Z=(98.2-98.6)/(0.62/√106) = -6.6423
P(X<98 .2="" 0="" 1.279017="" br="" decir="" es="" p="" practicamente="">
Por lo tanto
P(X
EVENTO
EVENTO: Dado un experimento aleatorio y su espacio muestral S, se llama Evento a un conjunto de resultados posibles de S. Fácilmente podemos notar que un evento, no es mas que un subconjunto de un espacio muestral.
EJERCICIOS RESUELTOS
En una encuesta hecha a la salida de la estación Cuauhtémoc del Metro, se supo que 53% de la gente lee el periódico “El Norte”, 50% lee el periódico “Milenio” y 15% no lee ninguno de estos periódicos. Si se escoge al azar a una persona:
1.1 ¿Cuál es la probabilidad de que lea ambos periódicos?
1.2 Dado que una persona lee el periódico “El Norte” ¿cuál es la probabilidad de que lea “Milenio”?
1.3 ¿Cuál es la probabilidad de que lea al menos uno de los dos periódicos?
2. Dado S = {México, España, Sierra Leona, Australia, Brasil, Canadá, Malta}
2.1 Indica el evento A “Países de América”
2.2 Indica el evento A’
2.3 Indica el evento B “Países de Europa”
2.4 Indica el evento A B
2.5 Indica el evento A B
2.6 Indica el evento (A B)’
2.7 ¿Cuál es la probabilidad de que un país no pertenezca a Europa o a América?
2.8 ¿Cuál es la probabilidad de que un país tenga como idioma el español?
1)
Eventos:
A --> Leer "El norte"
B --> Leer "Milenio"
P(A)=53% = 53/100 = 0.53
P(B)=50% = 50/100 = 0.50
P(no A y no B) = 15/100 = 0.15
1,1) Nos piden calcular P(A y B)
P(A o B) = P(A) + P(B) + P(A y B)
Sabemos que:
P(A)=0.53
P(B)=0.50
P(no A y no B) = 0.15 ---> Como P(A o B) = 1-P(no A y no B) --> Lo contrario de no leer ninguno es leer alguno que es lo mismo que leer uno u otro-->entonces
P(A o B)=1-0.15=0.85
Tenemos que
P(A o B) = P(A) + P(B) - P(A y B)
0.85 = 0.53 + 0.50 - P(A y B)
P(A y B) = 0.53 + 0.50 -0.85 = 0.18
La probabilidad que lean los dos periodicos es 0.18 --> 18%
1.2) Nos piden (B|A)
P(B|A) = P(A y B)/P(A) = 0.18 / 0.53 = 18/53 = 0.3396
1.3) Leer al menos un periodico es P(A o B) = 0.85 , como se ha calculado antes, por lo tanto, la probabilidad de leer algun periodico es 0.85 --> 85%
2)
2.1)
A ---> { México, Brasil, Canadá}
2.2)
A' es lo contrario de A es decir todos los paises menos los que no son de America
A' = { España,Sierra Leona, Australia, Malta}
2.3)
B --> { España,Malta }
2.4)
El evanto AB es A y B, es decir Paises de Ámerica y de Europa, no hay ninguno.
AB = { }
2.5) Lo mismo que 2.4
2.6)
(AB)' es lo contrario a A y B es decir lo contrario de ser de America y Europa,
(AB)' = {Australia,Sierra Leona}
2.7)
Tenemos 7 paises y 2 no son de Europa ni America {Sierra Leona, Australia} por o que la probabilidad buscada es 2/7 =0.2857 --> 28.57%
2.8)
De los 7 paises se habla español en 2 {Mexico,España} por lo que la probabilidad de que un pais tenga idioma español es
2/7 = 0.2857 --> 28.57%
EJERCICIOS RESUELTOS
En una encuesta hecha a la salida de la estación Cuauhtémoc del Metro, se supo que 53% de la gente lee el periódico “El Norte”, 50% lee el periódico “Milenio” y 15% no lee ninguno de estos periódicos. Si se escoge al azar a una persona:
1.1 ¿Cuál es la probabilidad de que lea ambos periódicos?
1.2 Dado que una persona lee el periódico “El Norte” ¿cuál es la probabilidad de que lea “Milenio”?
1.3 ¿Cuál es la probabilidad de que lea al menos uno de los dos periódicos?
2. Dado S = {México, España, Sierra Leona, Australia, Brasil, Canadá, Malta}
2.1 Indica el evento A “Países de América”
2.2 Indica el evento A’
2.3 Indica el evento B “Países de Europa”
2.4 Indica el evento A B
2.5 Indica el evento A B
2.6 Indica el evento (A B)’
2.7 ¿Cuál es la probabilidad de que un país no pertenezca a Europa o a América?
2.8 ¿Cuál es la probabilidad de que un país tenga como idioma el español?
1)
Eventos:
A --> Leer "El norte"
B --> Leer "Milenio"
P(A)=53% = 53/100 = 0.53
P(B)=50% = 50/100 = 0.50
P(no A y no B) = 15/100 = 0.15
1,1) Nos piden calcular P(A y B)
P(A o B) = P(A) + P(B) + P(A y B)
Sabemos que:
P(A)=0.53
P(B)=0.50
P(no A y no B) = 0.15 ---> Como P(A o B) = 1-P(no A y no B) --> Lo contrario de no leer ninguno es leer alguno que es lo mismo que leer uno u otro-->entonces
P(A o B)=1-0.15=0.85
Tenemos que
P(A o B) = P(A) + P(B) - P(A y B)
0.85 = 0.53 + 0.50 - P(A y B)
P(A y B) = 0.53 + 0.50 -0.85 = 0.18
La probabilidad que lean los dos periodicos es 0.18 --> 18%
1.2) Nos piden (B|A)
P(B|A) = P(A y B)/P(A) = 0.18 / 0.53 = 18/53 = 0.3396
1.3) Leer al menos un periodico es P(A o B) = 0.85 , como se ha calculado antes, por lo tanto, la probabilidad de leer algun periodico es 0.85 --> 85%
2)
2.1)
A ---> { México, Brasil, Canadá}
2.2)
A' es lo contrario de A es decir todos los paises menos los que no son de America
A' = { España,Sierra Leona, Australia, Malta}
2.3)
B --> { España,Malta }
2.4)
El evanto AB es A y B, es decir Paises de Ámerica y de Europa, no hay ninguno.
AB = { }
2.5) Lo mismo que 2.4
2.6)
(AB)' es lo contrario a A y B es decir lo contrario de ser de America y Europa,
(AB)' = {Australia,Sierra Leona}
2.7)
Tenemos 7 paises y 2 no son de Europa ni America {Sierra Leona, Australia} por o que la probabilidad buscada es 2/7 =0.2857 --> 28.57%
2.8)
De los 7 paises se habla español en 2 {Mexico,España} por lo que la probabilidad de que un pais tenga idioma español es
2/7 = 0.2857 --> 28.57%
TEOREMA DE BAYES (2022) Ejemplos
😁
TEOREMA DE BAYES: Es una preposicion planteada que expresa la probabilidad condicional de un evento aleatorio A dado B en terminos de la distribucion de probabilidad condicional del evento B dado A .
EJERCICIOS RESUELTOS
Problema 1
Dos maquina producen cada una la mitad de tornillos que produce la fabrica, la maquina A produce el 15 % de tornillos defectuosos y la B produce el 25%
Si la maquina C elige un tornillo al azar y resulta defectuoso ¿cual es la probabilidad de que:
a) Venga de la Maquina A
b) Venga de la Maquina B
Sucesos:
A: Tornillo producido por la maquina A
B: Tornillo producido por la maquina B
Como cada una produce la mitad de tornillos
=P(B)=0.5 "P(A)=P(B)=0.5")
D: Tornillo defectuoso Nos dice que:
=0.15\rightarrow "P(D/A)=0.15\rightarrow")
El 15 % de los tornillos de A son defectuosos
=0.25\rightarrow "P(D/B)=0.25\rightarrow")
El 25 % de los tornillos de B son defectuosos
Solución Inciso a)
Nos piden calcular "P(A/D)")
la probabilidad que si el tornillo es defectuoso  "(D)")
venga de la maquina A.
Por el Teorema de Bayes
=\frac{P(D/A)\ast&space;P(A)}{\left&space;\{&space;P(D/A\ast&space;P(A)+&space;P(D/B\ast&space;P(B)&space;\right&space;\}} "\bg_black P(A/D)=\frac{P(D/A)\ast P(A)}{\left \{ P(D/A\ast P(A)+ P(D/B\ast P(B) \right \}}")
=\frac{0.15\ast&space;0.5}{\left&space;\{&space;0.15\ast&space;0.5+&space;0.25\ast&space;0.5&space;\right&space;\}}=\frac{3}{8}=0.375 "\bg_black P(A/D)=\frac{0.15\ast 0.5}{\left \{ 0.15\ast 0.5+ 0.25\ast 0.5 \right \}}=\frac{3}{8}=0.375")
Solucion Inciso b)
Nos piden calcular "P(B/D)")
la probabilidad que si el tornillo es defectuoso venga de la maquina B.
Por el Teorema de Bayes
=\frac{P(D/B)\ast&space;P(B)}{\left&space;\{P(D/A)\ast&space;P(A)+&space;P(D/B)\ast&space;P(B)&space;\right&space;\}} "\bg_black P(B/D)=\frac{P(D/B)\ast P(B)}{\left \{P(D/A)\ast P(A)+ P(D/B)\ast P(B) \right \}}")
=\frac{0.25\ast&space;0.5}{\left&space;\{&space;0.15\ast&space;0.5+&space;0.25\ast&space;0.5&space;\right&space;\}}=\frac{5}{8}=0.625 "\bg_black P(A/D)=\frac{0.25\ast 0.5}{\left \{ 0.15\ast 0.5+ 0.25\ast 0.5 \right \}}=\frac{5}{8}=0.625")
Problema 2
Se recibieron dos cajas de camisas para hombre provenientes de la fabrica, La caja 1 contenia 25 camisas deportivas y 15 de vestir y la caja 2 30 deportivas y 10 de vestir . Se eligio a azar una caja y se selecciono aleatoriamente una camisa de esa caja para inspeccionarla y la camisa resulto ser deportiva ¿ Cual es la probabilidad de que la caja de la que proviene la camisa sea la caja uno?
Solución Inciso a)
 "C1\rightarrow Caja(1)")
 "C2\rightarrow Caja(2)")
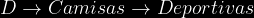
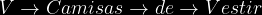
La probabilidad de escoger cualquier caja es:
=\frac{1}{2}=0.5 "P(C1)=\frac{1}{2}=0.5")
=\frac{1}{2}=0.5 "P(C2)=\frac{1}{2}=0.5")
Segun el enunciado la probabilidad de cada tipo de camisa en cada caja es:
=\frac{25}{25+15}=\frac{25}{40}=0.625 "P(D/C1)=\frac{25}{25+15}=\frac{25}{40}=0.625")
=\frac{15}{25+15}=\frac{15}{40}=0.375 "P(V/C1)=\frac{15}{25+15}=\frac{15}{40}=0.375")
=\frac{30}{30+10}=\frac{30}{40}=0.75 "P(D/C2)=\frac{30}{30+10}=\frac{30}{40}=0.75")
=\frac{10}{30+10}=\frac{10}{40}=0.25 "P(V/C2)=\frac{10}{30+10}=\frac{10}{40}=0.25")
Nos piden calcular cual es la probabilidad de que la caja de la que proviene la camisa sea la caja uno si ha salido una camisa deportiva es decir,
 "P(C1/D)")
Utilizando el Teorema de Bayes
=\frac{P(D/C1)\ast&space;P(C1)}{\left&space;\{P(D/C1)\ast&space;P(C1)+&space;P(D/C2)\ast&space;P(C2)&space;\right&space;\}} "\bg_black P(C1/D)=\frac{P(D/C1)\ast P(C1)}{\left \{P(D/C1)\ast P(C1)+ P(D/C2)\ast P(C2) \right \}}")
=\frac{0.625\ast&space;0.5}{\left&space;\{&space;0.625\ast&space;0.5+&space;0.75\ast&space;0.5&space;\right&space;\}}= "\bg_black P(C1/D)=\frac{0.625\ast 0.5}{\left \{ 0.625\ast 0.5+ 0.75\ast 0.5 \right \}}=")
=0.4545 "P(C1/D)=0.4545")
La probabilidad buscada es de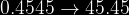
%
EJERCICIOS RESUELTOS
Problema 1
Dos maquina producen cada una la mitad de tornillos que produce la fabrica, la maquina A produce el 15 % de tornillos defectuosos y la B produce el 25%
Si la maquina C elige un tornillo al azar y resulta defectuoso ¿cual es la probabilidad de que:
a) Venga de la Maquina A
b) Venga de la Maquina B
Sucesos:
A: Tornillo producido por la maquina A
B: Tornillo producido por la maquina B
Como cada una produce la mitad de tornillos
D: Tornillo defectuoso Nos dice que:
Solución Inciso a)
Nos piden calcular
Por el Teorema de Bayes
Solucion Inciso b)
Nos piden calcular
Por el Teorema de Bayes
Problema 2
Se recibieron dos cajas de camisas para hombre provenientes de la fabrica, La caja 1 contenia 25 camisas deportivas y 15 de vestir y la caja 2 30 deportivas y 10 de vestir . Se eligio a azar una caja y se selecciono aleatoriamente una camisa de esa caja para inspeccionarla y la camisa resulto ser deportiva ¿ Cual es la probabilidad de que la caja de la que proviene la camisa sea la caja uno?
Solución Inciso a)
La probabilidad de escoger cualquier caja es:
Segun el enunciado la probabilidad de cada tipo de camisa en cada caja es:
Nos piden calcular cual es la probabilidad de que la caja de la que proviene la camisa sea la caja uno si ha salido una camisa deportiva es decir,
Utilizando el Teorema de Bayes
La probabilidad buscada es de
HIPOTESIS
1. Con gasolina de la marca A, el número medio de millas por galón que recorren 5 automóviles similares en igualdad de condiciones es 22.6 con desviación típica 0.48. Con gasolina de otra marca B, el resultado es 21.4 con desviación típica 0.54. Usando un nivel de significación 0.05, investigar si la marca A es de mejor calidad que la B
1)
tenemos que
Xa=22.6
Xb=21.4
σa=0.48
σb=0.54
n=5
alfa=0.05
Ho : μa - μa=0
H1 : μa - μb>0
Calculamos el estadistico
T=(Xa-Xb-0)/√(σa²/n1+σb²/n2)
Z=(22.6-21.4)/√(0.48²/5+0.54²/5) = 3.71
El p-valor es
P(Z>3.71) = 1-P(Z<3 .71="" 1-0.9999="0.0001<br">
Como 0.0001 es menor que la significación 0.05 rechazamos la hipotesis nula y aceptamos la alternativa : que la marca A es de mejor calidad que B
2) Dos tipos de soluciones química A Y B, han sido probadas para ver su pH (grado de acidez de la solución). el análisis de 6 muestras de A arroja un pH medio de 7.52 con desviación típica 0.024, mientras que 5 muestras de de B dan un pH medio de 7.49 con desviación típica 0.032 usando el nivel de significación 0.05, determinar si los dos tipos de soluciones tienen distinto pH.
2)
tenemos que
Xa=7.52
Xb=7.49
σa=0.024
σb=0.032
n1=6
n2=5
alfa=0.05
Ho : μa - μa=0
H1 : μa - μb≠0
Calculamos el estadistico
T=(Xa-Xb-0)/√(σa²/n1+σb²/n2)
Z=(7.52-7.49)/√(0.024²/6+0.032²/5) = 1.73
El p-valor es
2*P(Z>|1.73|) = 2*(1-P(Z<1 .73="" 0.0836="" 0.9582="" 2="" br="">
como 0.0836 es mayor que la significación 0.05, no podemos rechazar la hipotesis nula por lo que concluimos que los dos tipos de soluciones tienen el mismo pH
1)
tenemos que
Xa=22.6
Xb=21.4
σa=0.48
σb=0.54
n=5
alfa=0.05
Ho : μa - μa=0
H1 : μa - μb>0
Calculamos el estadistico
T=(Xa-Xb-0)/√(σa²/n1+σb²/n2)
Z=(22.6-21.4)/√(0.48²/5+0.54²/5) = 3.71
El p-valor es
P(Z>3.71) = 1-P(Z<3 .71="" 1-0.9999="0.0001<br">
Como 0.0001 es menor que la significación 0.05 rechazamos la hipotesis nula y aceptamos la alternativa : que la marca A es de mejor calidad que B
2) Dos tipos de soluciones química A Y B, han sido probadas para ver su pH (grado de acidez de la solución). el análisis de 6 muestras de A arroja un pH medio de 7.52 con desviación típica 0.024, mientras que 5 muestras de de B dan un pH medio de 7.49 con desviación típica 0.032 usando el nivel de significación 0.05, determinar si los dos tipos de soluciones tienen distinto pH.
2)
tenemos que
Xa=7.52
Xb=7.49
σa=0.024
σb=0.032
n1=6
n2=5
alfa=0.05
Ho : μa - μa=0
H1 : μa - μb≠0
Calculamos el estadistico
T=(Xa-Xb-0)/√(σa²/n1+σb²/n2)
Z=(7.52-7.49)/√(0.024²/6+0.032²/5) = 1.73
El p-valor es
2*P(Z>|1.73|) = 2*(1-P(Z<1 .73="" 0.0836="" 0.9582="" 2="" br="">
como 0.0836 es mayor que la significación 0.05, no podemos rechazar la hipotesis nula por lo que concluimos que los dos tipos de soluciones tienen el mismo pH
Suscribirse a:
Entradas (Atom)