miércoles, 10 de febrero de 2021
PROBABILIDAD (2024)
Temas de Probabilidad:
Definicion de Probabilidad
Distribución Exponencial
Distribución de Poisson
Distribución Geometrica
Distribución Hipergeometrica
Distribución Binomial
Distribución Uniforme
Combinación
Teorema de Bayes
Distribución Binomial por la de Poisson
Distribución Normal
Variable Aleatoria Continua
Variable Aleatoria Discreta
Sucesos
Eventos
CALCULO DIFERENCIAL
Temas de Calculo Diferencial
Funciónes y limites
Continuidad de una Función
Derivada de una Función.
Aplicaciones de la Derivada.
Otros Usos de la Derivada.
domingo, 3 de noviembre de 2019
INTEGRACION POR CAMBIO DE VARIABLE
Integral por cambio de variable
Solución:
Se utiliza la formula 
Donde
Analisis
Sustituyendo los valores en la formula:
Se realiza el cambio de variable
domingo, 27 de octubre de 2019
DEFINICION DE PROBABILIDAD(2022)
Historia de Probabilidad
¿QUE ES PROBABILIDAD?
¿QUE ES PROBABILIDAD?
El ser humano siempre ha estado en contacto con situaciones aleatorias, ya sea de experiencias naturales o juego que el mismo crea, en donde prevalece la incertidumbre por ejemplo, se han encontrado en las tumbas egipcias restos de dados cúbicos con marcas idénticas a las de los dados actuales que datan del año 2000 a.c, mas aun se tienen indicios que aproximadamente por el año 3500 a.c los egipcios tenían juegos de azar que practicaban con objetos de huesos.
Por tales razones el estudio de la incertidumbre siempre ha tenido interés particular para la humanidad, desde conocer la incertidumbre con respecto del clima, el resultado del lanzamiento de una moneda o un dado, hasta situaciones modernas, como son el curso del cambio de la moneda nacional, la bolsa de valores para conocer en que acciones se tiene mayor o menor riesgo en su inversión.
Así, desde su aparición los juegos de incertidumbre han dejado un gran reto a diferentes matemáticos para calcular las probabilidades de exito que tiene un jugador en un juego de azar, de tal forma que haciendo un poco de historia resulta que la creación de la probabilidad se atribuye a los matemáticos franceses del siglo XVII Blaise Pascal (1623-1662) y Pierre de Fermat (1601-1665) cuando lograron obtener probabilidades exactas para ciertos tipos de problemas relacionados con los juegos de los dados. aunque algunos matemáticos anteriores como Geloramo Cardano en el siglo XVI (1501-1576) y Galileo Galilei (1564-1642) , habían aportado importantes contribuciones a su desarrollo calculando algunas combinaciones numéricas para ciertos problemas relacionados con los dados.
Uno de los problemas clásicos con los que dio inicio el calculo de las probabilidades consiste en saber cuantos dados hay que lanzar para que la probabilidad de que salga algún seis supere el 50 % .
Actualmente se tiene una gran cantidad de juegos al azar para los cuales se requiere realizar ciertos calculos de probabilidad por ejemplo la lotería el melate el tris etc.
La historia nos muestra que la teoría de probabilidad dios sus primeros pasos en el siglo XVI con Geloramo Cardano y Galileo Galilei posteriormente en el siglo XVII con Blaise Pascal Pierre de Fermat , Jean y Jacques Bernoulli (1654-1705), De Moivre (1667-1754) en el siglo XVIII Daniel bernoulli (1700-1782),Kart Friedrich Gauss (1777-1855) Siemon denis poisson (1781-1840) en el siglo XX A. Marcov, Chebyschev,Liapunov etc, pero quien sento las bases teóricas para formalizar el desarrollo de la teoria de las probabilidades fue el matemático ruso A. Kolmogorov en 1933 al introducir la teoria de la medida en el calculo de las probabilidades.
Durante todo el texto estaremos hablando de probabilidad, pero que podemos entender de esta ciencia.
CONCEPTO DE PROBABILIDAD:
Rama de las matemáticas que se ocupa para medir o determinar cuantitativamente la posibilidad de que ocurra un determinado suceso.
Así veremos en el desarrollo del texto, principalmente en los 3 primeros capítulos, que en general, la probabilidad esta basada en el estudio de combinatoria, ampliándose al Calculo con el uso de las funciones
Actualmente la teoría de las probabilidades es una herramienta importante en la mayoría de las áreas de la ingeniería ciencias y administración de tal forma que realizar un estudio adecuado de la probabilidad es fundamental para el éxito de muchas compañías en particular las compañías de seguro ya que están evalúan las probabilidades de los sucesos que les interesan como por ejemplo
accidentes de coches, inundaciones, epidemias. mediante una minuciosa recopilación de datos experiencias que les permitan inferir dichas probabilidades con suficiente aproximación como para poder asignar las cuotas de manera justa, ademas de las compañías de seguros tenemos aplicaciones a la medicina, meteorología, mercadotecnia, mediciones de predicciones de terremotos, comportamiento humano, finanzas.
lunes, 2 de marzo de 2015
DISTRIBUCION EXPONENCIAL (2022) Ejemplos
El tiempo Y que tarda en realizarse cierta tarea clave en la construccion de una casa es una variable aleatoria que tiene una distribucion exponencial con una media de 10 horas.
El costo C para completar esta tarea esta relacionado con Y mediante
C = 100 + 40Y + 3Y2
Encontrar el valor esperado y la varianza de C.
f(y) = k e^(- k y) para y > 0
μ = ∫ k y e^(- k y) = 1/ k de 0 a infinito
μ = 10 ---> k = 0.1 ..........var(y) = 1/ k^2 = 1/ .01 = 100
El valor esperado de y^2
∫ .1y^2 e^( - .1y) = 200 de o a infinito
E(C) = 100+40 E(y) + 3 E(y^2)
E(C) = 100 + 40 (10) + 3 (200)
E(C) = 100 + 400 + 600 = 1100
Para la varianza me falta tiempo.
Var(C) = E ( C - E(C))^2
C - E(C) = 100 + 40 y + 3 y^2 - (100 + 40 E(y) + 3 E(y^2))
E(C - E(C))^2 =( 40 y + 3 y^2 - 40(10) + 3 (200) )^2
Var(C) = E(1000000 - 80000 y - 4400 y^2 + 240 y^3 + 9 y^4)
Var(C) = 1000000 -80000E(y) -4400E(y^2) + 240E(y^3) + 9E(y^4)
E(y^3)= ∫ .1y^3 e^( - .1y) = 6000 de o a infinito
E(y^4) = ∫ .1y^4 e^( - .1y) = 240000 de o a infinito
= 1000000 - 80000(10) - 4400(200) + 240(6000) + 9(240000)
Var(C) = 2 920 000
El costo C para completar esta tarea esta relacionado con Y mediante
C = 100 + 40Y + 3Y2
Encontrar el valor esperado y la varianza de C.
f(y) = k e^(- k y) para y > 0
μ = ∫ k y e^(- k y) = 1/ k de 0 a infinito
μ = 10 ---> k = 0.1 ..........var(y) = 1/ k^2 = 1/ .01 = 100
El valor esperado de y^2
∫ .1y^2 e^( - .1y) = 200 de o a infinito
E(C) = 100+40 E(y) + 3 E(y^2)
E(C) = 100 + 40 (10) + 3 (200)
E(C) = 100 + 400 + 600 = 1100
Para la varianza me falta tiempo.
Var(C) = E ( C - E(C))^2
C - E(C) = 100 + 40 y + 3 y^2 - (100 + 40 E(y) + 3 E(y^2))
E(C - E(C))^2 =( 40 y + 3 y^2 - 40(10) + 3 (200) )^2
Var(C) = E(1000000 - 80000 y - 4400 y^2 + 240 y^3 + 9 y^4)
Var(C) = 1000000 -80000E(y) -4400E(y^2) + 240E(y^3) + 9E(y^4)
E(y^3)= ∫ .1y^3 e^( - .1y) = 6000 de o a infinito
E(y^4) = ∫ .1y^4 e^( - .1y) = 240000 de o a infinito
= 1000000 - 80000(10) - 4400(200) + 240(6000) + 9(240000)
Var(C) = 2 920 000
FRACCIONES
FRACCIÓN COMÚN: Es una expresión que representa una o varias partes de la unidad; también se le denomina "QUEBRADO".
Una fracción esta compuesta de dos números llamados términos de la fracción y separados entre si por medio de una lineal horizontal o diagonal.
Una fracción esta compuesta de dos números llamados términos de la fracción y separados entre si por medio de una lineal horizontal o diagonal.
El numero que va sobre la linea, se llama NUMERADOR
El que va por debajo de la linea, se llama DENOMINADOR
Ejemplo:
FRACCIÓN PROPIA: Su valor es menor a la unidad.
Ejemplo:
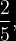
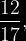
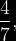
FRACCIÓN IMPROPIA: Su valor es mayor o igual que la unidad.
Ejemplo:
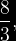
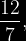
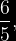
NUMERO MIXTO: Se llama numero mixto al que esta formado por una parte entera y una fraccionaria. Para transformar fracciones impropias en números mixtos, solo es necesario realizar la división.
para transforma esta fracción impropia tenemos que hacer una división.
Lo cual nos da como resultado la división de 5 entre 2 una fracción mixta que es 2 enteros 1 medio.
\left&space;(&space;7&space;\right&space;)+5}{7}=\frac{21+5}{7}=\frac{26}{7} "3\frac{5}{7}=\frac{\left ( 3 \right )\left ( 7 \right )+5}{7}=\frac{21+5}{7}=\frac{26}{7}")
DEFINICION DE NUMERADOR: Es el numero que indica cuantas unidades fraccionarias contiene la fracción.
DEFINICION DE DENOMINADOR: Es el numero que indica las partes iguales en que se ha dividido la unidad.
Las fracciones comunes se clasifican en fracción propia y fracción impropia.
FRACCIÓN PROPIA: Su valor es menor a la unidad.
Ejemplo:
FRACCIÓN IMPROPIA: Su valor es mayor o igual que la unidad.
Ejemplo:
EJERCICIOS RESUELTOS
👉 Problema 01: 😆
Transformar una fracción impropia a una mixta
👉 Problema 02: 😆
Transformar un numero mixto a una fracción impropia
Para la solución de este problema hacemos la multiplicación del denominador del numero mixto que es 7 por el numero entero que es 3 mas la suma del numerador que es 5 todo esto entre 7 la cual nos da como resultado en la imagen siguiente:
DISTRIBUCION EXPONENCIAL
El tiempo de recurrencia para el tratamiento de cierto tipo de cáncer es una variable aleatoria con una distribución exponencial con media λ. 50% de los pacientes tienen una recurrencia dentro de 693 días.
a)Encuentre λ
b)Encuentre la probabilidad de que un paciente que no ha tenido la recurrencia en el primer año después del tratamiento, tendrá la recurrencia durante el segundo año.
la distribución exponencial tiene por función de densidad:
f(x) = 1/λ * exp(-1/λ*x)
La función de distribución (probabilidad acumulada) es
P(X<=x) = F(X) = 1 - exp(-1/λ*x)
Nos dicen que
F(693) = 0.50
1 - exp(-1/λ*693) = 0.50
exp(-1/λ*693) = 1-0.50
exp(-1/λ*693) = 0.50
tomando logaritmos
ln { exp(-1/λ*693) } = ln 0.50
-1/λ*693 = ln 0.50
-693/λ = ln 0.50
λ = -693 / ln 0.50
λ = 999.77
b)
Es una probabilidad condicionada
P(365365) = P(365365)
365
por tanto la probabildad es
P(365X<730>365) =
donde
P(365X<730 -="" f="" p="">
P(X>365) = 1-F(365)
tenemos que
F(730) = 1-exp(-1/999.78*730) = 0.5182
F(365) = 1-exp(-1/999.78*365) = 0.3059
Por tanto
P(365X<730 -="" 0.3059="0.2123</p" 0.5182="" f="">
P(X>365) = 1-F(365) = 1-0.3059 = 0.6941
La probabilidad es 0.2123/0.6941 = 0.3058
a)Encuentre λ
b)Encuentre la probabilidad de que un paciente que no ha tenido la recurrencia en el primer año después del tratamiento, tendrá la recurrencia durante el segundo año.
la distribución exponencial tiene por función de densidad:
f(x) = 1/λ * exp(-1/λ*x)
La función de distribución (probabilidad acumulada) es
P(X<=x) = F(X) = 1 - exp(-1/λ*x)
Nos dicen que
F(693) = 0.50
1 - exp(-1/λ*693) = 0.50
exp(-1/λ*693) = 1-0.50
exp(-1/λ*693) = 0.50
tomando logaritmos
ln { exp(-1/λ*693) } = ln 0.50
-1/λ*693 = ln 0.50
-693/λ = ln 0.50
λ = -693 / ln 0.50
λ = 999.77
b)
Es una probabilidad condicionada
P(365
365
por tanto la probabildad es
P(365X<730>365) =
donde
P(365X<730 -="" f="" p="">
P(X>365) = 1-F(365)
tenemos que
F(730) = 1-exp(-1/999.78*730) = 0.5182
F(365) = 1-exp(-1/999.78*365) = 0.3059
Por tanto
P(365X<730 -="" 0.3059="0.2123</p" 0.5182="" f="">
P(X>365) = 1-F(365) = 1-0.3059 = 0.6941
La probabilidad es 0.2123/0.6941 = 0.3058
DISTRIBUCION EXPONENCIAL
La vida promedio de un televisor es de 12 años. La vida de los productos sigue con frecuencia, una distribucion exponencial de probabilidad suponga que es el caso del televisor.
Cual es la probabilidad de que la vida sea de 15 años o mas.
E(X)=1/λ
12=1/λ
λ=1/12
La formula de la distribución exponencial es
f(x)=λ*exp(-λx)
y la de probabilidad acumulada e
F(x)=1-exp(-λx) que representa a P(X≤x)
a)
Debemos calcular
P(X>15) = 1 - P(X≤15) = 1-F(15)
F(15)= 1-exp(-1/12*15) = 0.7135
por lo que
P(X>15) = 1-F(15) = 1-0.7135
P(X>15) = 0.2865
Cual es la probabilidad de que la vida sea de 15 años o mas.
E(X)=1/λ
12=1/λ
λ=1/12
La formula de la distribución exponencial es
f(x)=λ*exp(-λx)
y la de probabilidad acumulada e
F(x)=1-exp(-λx) que representa a P(X≤x)
a)
Debemos calcular
P(X>15) = 1 - P(X≤15) = 1-F(15)
F(15)= 1-exp(-1/12*15) = 0.7135
por lo que
P(X>15) = 1-F(15) = 1-0.7135
P(X>15) = 0.2865
FUNCIONES Y LIMITES
FUNCIÓN: Es el conjunto de pares ordenados de números reales (x,y) en los que el primer elemento es diferente en todos y cada uno de los pares ordenados.
Ejemplo:
1-A =(2,5)(3,6)(4,7)(5,8) Representa una función ya que el primer elemento de cada par ordenado es diferente de los otros.
2-B=(1,1)(1,-1)(4,2)(4,-2) No representa una función ya que se repite el primer elemento en ciertos pares ordenados.
REGLA DE CORRESPONDENCIA
Es la expresión que relaciona la variable dependiente con la variable independiente y se denota por:
y= F(x),se lee (y es igual a f de x )
Donde:
x: variable independiente
y:variable dependiente
F(x):regla de correspondencia
Ejemplo:
1-A =(2,5)(3,6)(4,7)(5,8) Representa una función ya que el primer elemento de cada par ordenado es diferente de los otros.
2-B=(1,1)(1,-1)(4,2)(4,-2) No representa una función ya que se repite el primer elemento en ciertos pares ordenados.
REGLA DE CORRESPONDENCIA
Es la expresión que relaciona la variable dependiente con la variable independiente y se denota por:
y= F(x),se lee (y es igual a f de x )
Donde:
x: variable independiente
y:variable dependiente
F(x):regla de correspondencia
DIVISIBILIDAD Y CALCULO DEL MAXIMO COMUN DIVISOR
DIVISIBILIDAD: Un numero es divisible entre otro cuando al dividir el primero entre el segundo, el cociente es exacto.
EJEMPLOS: La divisibilidad es la propiedad que tiene un numero para ser dividido entre otro exactamente.
CRITERIOS DE DIVISIBILIDAD: En ciertos casos no es necesario efectuar la división, basta seguir los criterios de divisibilidad que a continuación se señalan.
NUMERO PAR: Es todo numero que es múltiplo de 2
EJEMPLO: Son números pares: 2,4,6,8,10,12,14....etc
NUMERO IMPAR: Es todo numero que no es múltiplo de 2
EJEMPLO: Son números impares: 1,3,5,7,9,11,13,15.....etc
EJEMPLOS: La divisibilidad es la propiedad que tiene un numero para ser dividido entre otro exactamente.
CRITERIOS DE DIVISIBILIDAD: En ciertos casos no es necesario efectuar la división, basta seguir los criterios de divisibilidad que a continuación se señalan.
NUMERO PAR: Es todo numero que es múltiplo de 2
EJEMPLO: Son números pares: 2,4,6,8,10,12,14....etc
NUMERO IMPAR: Es todo numero que no es múltiplo de 2
EJEMPLO: Son números impares: 1,3,5,7,9,11,13,15.....etc
NUMEROS MULTIPLOS,COMPUESTOS Y PRIMOS
MÚLTIPLO DE UN NUMERO: Un numero A es múltiplo de un numero B si al efectuar la división A/B esta es exacta, es decir, el residuo es cero.
EJEMPLOS:
NÚMEROS COMPUESTOS: Es todo numero natural distinto de la unidad y que puede ser expresado como el producto de dos o más enteros positivos diferentes de si mismo, los cuales son sus factores y en algunos casos pueden repetirse.
EJEMPLOS:
4 se puede factorizar en: (2)(2) ó (4)(1).
6 se puede factorizar en: (3)(2) ó (6)(1).
8 se puede factorizar en: (4)(2) ó (8)(1) ó (2)(2)(2).
26 se puede factorizar en: (13)(2) ó (26)(1).
EJEMPLOS:
NÚMEROS COMPUESTOS: Es todo numero natural distinto de la unidad y que puede ser expresado como el producto de dos o más enteros positivos diferentes de si mismo, los cuales son sus factores y en algunos casos pueden repetirse.
EJEMPLOS:
4 se puede factorizar en: (2)(2) ó (4)(1).
6 se puede factorizar en: (3)(2) ó (6)(1).
8 se puede factorizar en: (4)(2) ó (8)(1) ó (2)(2)(2).
26 se puede factorizar en: (13)(2) ó (26)(1).
MINIMO COMUN MULTIPLO
MÍNIMO COMÚN MÚLTIPLO: Un entero es un múltiplo común de dos o mas enteros dados si es múltiplo de cada uno de ellos. Es frecuente tener que usar el menor entero positivo que sea común múltiplo de dos o mas enteros,al cual se le llama mínimo común múltiplo y se simboliza por m.c.m ó M.C.M.
PASOS PARA DETERMINAR EL M.C.M.
1- Se halla la factorización prima de cada número.
2-El M.CM. se forma con el producto de los factores primos comunes y no comunes afectados con su mayor exponente.
EJEMPLOS:
Hallar el m.c.m de 18,24 y 15
PASOS PARA DETERMINAR EL M.C.M.
1- Se halla la factorización prima de cada número.
2-El M.CM. se forma con el producto de los factores primos comunes y no comunes afectados con su mayor exponente.
EJEMPLOS:
Hallar el m.c.m de 18,24 y 15
VALOR ABSOLUTO
VALOR ABSOLUTO: El valor absoluto de x denotado por /x/ indica la magnitud de x sin considerar su signo; existe un valor absoluto dentro de los números el cual es independiente de su posición en la recta así el valor absoluto de un numero cualquiera es la distancia del 0 al numero en cuestión sin tomar en cuenta el sentido positivo o negativo.
Ejemplo:
Ejemplo:
El valor absoluto de todo un numero entero es la distancia que existe entre éste y el cero y se representa como /x/.
Suscribirse a:
Comentarios (Atom)